guias para exercícios

IC para um parâmetro

graph TD P[Qual o parâmetro?] -->|média populacional| DMED[Qual a distribuição?]; P -->|variância populacional| DVAR[Qual a distribuição?]; P -->|proporção populacional| DIMBERNOULLI[Qual a dimensão?]; DMED -->|X segue Normal| DMEDNORMAL[Que a variância?]; DMED -->|X segue Genérica| DMEDGENERICA[Qual a dimensão?]; DMEDNORMAL -->|var. populacional| ZIC[Z interval]; DMEDNORMAL -->|var. amostral| tIC[t interval]; DMEDGENERICA -->|n>=30| DMEDGENERICAZINTERVAL[Z interval, aprox]; DMEDGENERICA -->|n<30| DMEDGENERICANAOP[IC não paramétrico]; DIMBERNOULLI -->|n>=30| ONEPROPZINTER[1 prop Z interval]; DIMBERNOULLI -->|n<30| ONEPROP[IC não paramétrico];

TH para uma v.a.

Matéria abordada no Capítulo 3 da UC sobre inferência estatística em uma única variável aleatória (uma única população).

graph TD POP[Qual a população?] -->|X segue Normal| IPN[Qual o parâmetro?]; POP -->|X segue Genérica| IPG[Qual a dimensão?]; POP -->|X segue Bernoulli| IPP[Qual a dimensão?]; IPN -->|TH média| IPNMEDIA[Qual a variância?]; IPN -->|TH variância| IPNVAR[X^2 test]; IPNMEDIA -->|var. populacional| IPNMEDIAZTEST[Z Test]; IPNMEDIA -->|var. amostral| IPNMEDIATTEST[t Test]; IPG -->|n>=30| IPGTLC[Qual a variância?]; IPGTLC -->|var. populacional| IPGTLCZ[Z test, aprox.] IPGTLC -->|var. amostral| IPGTLCZ[Z test, aprox.] IPG -->|n<30| NAOP[testes não paramétricos]; IPP -->|n>=30| IPPTLC[proporção p]; IPP -->|n<30| NAOP; IPPTLC --> ZTESTPROP[1-prop z test];

Qual a população no enunciado?

1 POPULAÇÃO NORMAL

Assume-se que \(X \sim \text{normal}\)

1.1 O enunciado pede um TH, ou IC, para a média (\(\mu\))?

1.1.1 A variância populacional, \(\sigma^2\), é conhecida?

Assume-se que \(X \sim \text{normal}(\mu,\; \sigma^2)\) com \(\sigma^2\) dada no enunciado.

Ligações úteis:

• teste e intervalo Z para a média (IC, teste com p-value, teste com RC, teste com IC)

• distribuição de amostragem Normal

• calculadora gráfica

1.1.2 A variância populacional, \(\sigma^2\), é desconhecida?

Assume-se que \(\sigma^2\) é desconhecida

Ligações úteis:

• teste e intervalo t para a média (IC, teste com p-value, teste com RC, teste com IC)

• distribuição de amostragem t-Student

• calculadora gráfica

1.2 O enunciado pede um TH, ou IC, para a variância ou desvio padrão populacional (\(\sigma\))?

1.2.1 TH ou IC para a variância populacional (\(\sigma^2\))?

Assume-se que \(X \sim \text{normal}(\mu,\; \sigma^2)\) em que ambos os parâmetros são desconhecidos.

Ligações úteis:

• TH e IC do qui-quadrado para a variância (IC, teste com p-value, teste com RC, teste com IC)

• distribuição de amostragem qui-quadrado

• calculadora gráfica

1.2.2 TH ou IC para o desvio padrão populacional (\(\sigma\))?

Assume-se que \(X \sim \text{normal}(\mu,\; \sigma^2)\) em que ambos os parâmetros são desconhecidos.

Etapas para o IC:

1. Obter IC para a variância populacional (\(\sigma^2\)).

2. Obter IC para o desvio padrão populacional (\(\sigma\)) usando a raiz do intervalo para a variância

Etapas para um TH:

1. Fazer o TH para a variância populacional (\(\sigma^2\)).

2. A conclusão é idêntica para o desvio padrão populacional (\(\sigma\)).

Ligações úteis:

• TH e IC do qui-quadrado para a variância (IC, teste com p-value, teste com RC, teste com IC)

• distribuição de amostragem qui-quadrado

• calculadora gráfica

2 POPULAÇÃO GENÉRICA

Diz-se que a população é genérica quando não é possível identificar a população através do enunciado. Assume-se que \(X \sim \text{generica}\).

Assume-se que \(n \ge 30\).

2.1. Com variância populacional conhecida (\(\sigma^2\))?

Assume-se que \(\sigma^2\) é conhecida.

Ligações úteis:

• inferência em população genérica (IC, teste com p-value, teste com RC, teste com IC)

• calculadora gráfica

2.2. Só se conhecem medidas amostrais?

Assume-se que \(\sigma^2\) é desconhecido.

Faz-se: \(\hat \sigma^2 = s_c^2\) pois n é elevado.

Ligações úteis:

• inferência em população genérica (IC, teste com p-value, teste com RC, teste com IC)

• calculadora gráfica

3 POPULAÇÃO de BERNOULLI (IC e TH em proporções)

Ligações úteis:

• inferência sobre proporções (IC, teste com p-value, teste com RC, teste com IC)

• calculadora gráfica

Ajustamento à Normal (QQPlot e Testes)

Consulte os procedimentos para testar o ajustamento à normal para testar o ajustamento dos dados à normal ou o guia de interpretação de enunciados.

TH para comparação de médias de duas v.a.

• Comparação de duas v.a., X e Y, com distribuição normal:

  • duas amostras emparelhadas (t test) - dado um indivíduo, o peso antes, \(X_i\), e o peso depois, \(Y_i\), de uma dieta;

  • duas amostras independentes (t test) - sempre que não haja emparelhamento

graph TD TIPO[Qual o tipo de teste?] -->|amostras normais emparelhadas| EMP[1 var. teste t, variável D=X-Y]; TIPO -->|amostras normais independentes| VKNOWN[Var. pop. conhecidas?]; VKNOWN -->|sim| INDCONHECIDAS[2 vars Z test]; VKNOWN -->|não| TESTEF[Teste F de Fisher]; TESTEF -->|variâncias iguais| INDIGUAIS[2 vars. teste t com Pooled=yes]; TESTEF -->|variâncias diferentes| INDDIF[2 vars. teste t com Pooled=no];

Referências:

• duas amostras emparelhadas (t test) («1 var. teste t, variável D=X-Y»)

• duas amostras independentes (t test)

• distribuição F de Fisher e homogeneidade de duas variâncias (teste F)

• teste a duas proporções independentes (não está no esquema acima).

ANOVAs

As ANOVAs introduzidas, nesta documentação, são:

graph TD TIPO[Quantos grupos independentes?] -->|dois| TESTET[teste t de 2 vars.]; TIPO[Quantos grupos independentes?] -->|três ou mais| ANOVA[Efetuar ANOVA]; ANOVA -->|independência em todas as obser.| AINDEP[Quantos fatores?]; ANOVA -->|dependência| AMR[ANOVA Medidas Repetidas]; AINDEP -->|1 fator| A1F[ANOVA 1 fator]; AINDEP -->|2 fatores| A2F[ANOVA 2 fatores]; A1F -->|efeitos fixos| CMPMUL[Comparações Múltiplas]; A1F -->|efeitos aleatórios| A1FFIM[Não se faz CM]; A2F -->|efeitos fixos| CMPMUL; CMPMUL -->|tende para H0| CMPMULBON[Bonferroni]; CMPMUL -->|tende para H1| CMPMULTUK[Tukey];

(Existem mais métodos ANOVA para as diversificadas situações.)

Referências:

• anova e o que é o teste anova?

• anova a 1 fator

• anova a 2 fatores

• homogeneidade das variâncias dos grupos

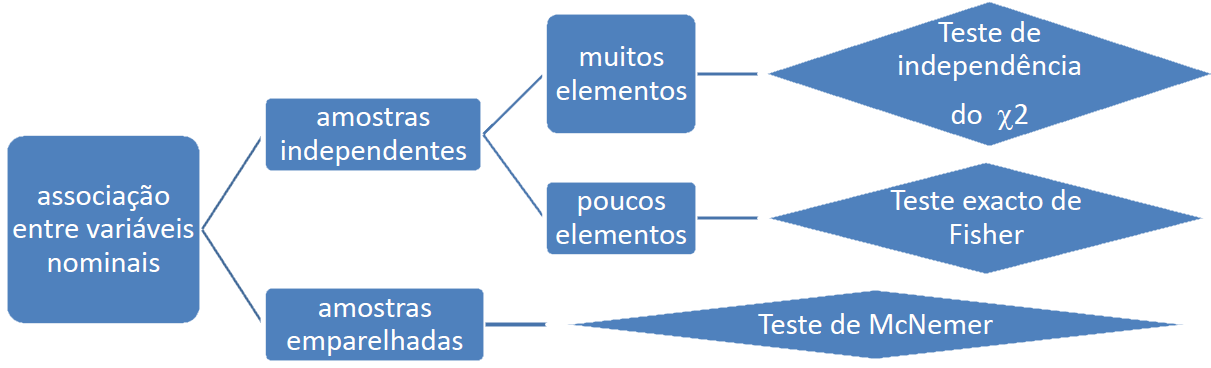
correlação

Esquema

graph TD AM[Amostras] -->|não emparelhadas| TC[ver Tabelas de Contingência]; AM[Amostras] -->|emparelhadas| EMP[teste à correlação]; EMP -->|ordinal ou não normal ou não linear| SP[Coef. de Spearman]; EMP -->|razões e normal e linear| PE[Coef. de Pearson];

Aplicar o correlação de Spearman quando uma das situações ocorre:

• as variáveis estão pelo menos na escala de ordinal (por exemplo, «mau», «médio», «bom», e também escala de razões), ou,

• as variáveis não seguem uma distribuição normal, ou,

• o gráfico de dispersão sugere uma correlação não linear.

Aplicar o correlação de Pearson quando todas as situações ocorrem:

• as variáveis estão pelo menos na escala de razões (e também intervalos), e,

• as variáveis seguem uma distribuição normal, e,

• o gráfico de dispersão sugere uma correlação linear.

Ver testes em tabelas de contingência.

Esquema abrangente

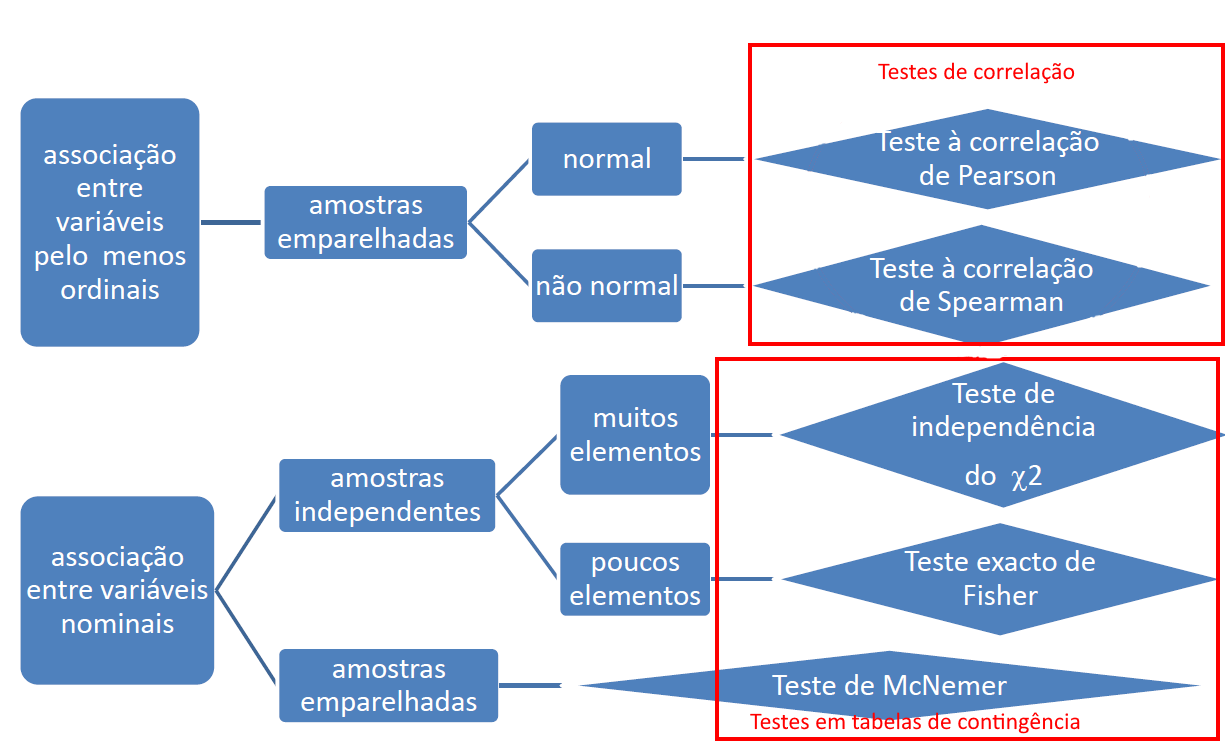
testes em tabelas de contingência