distribuição F de Fisher
A distribuição F de Fisher é usada para inferência sobre a comparação de duas variâncias tendo duas aplicações, no contexto desta documentação:
na comparação de duas variâncias amostrais como pré-teste da comparação de médias de duas amostras independentes (t test);
na técnica da anova, em que é efetuada a comparação entre a variação produzida por um fator e a variação produzida pelos «erros».
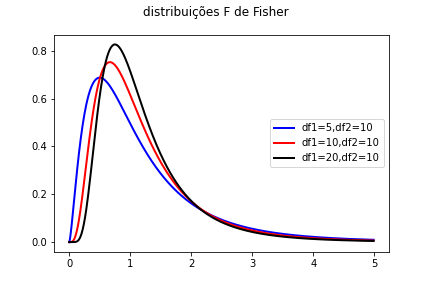
Cada distribuição F é caracterizada pelos graus de liberdade df1 e df2 (habitualmente os graus de liberdade da variância associada do numerador e do denominador). É assimétrica positiva tornam-se quase simétrica, em torno de 1, à medida que df1 e df2 tendem a infinito.
Uma situação usual é a seguinte: quando se obtém um quantil, deseja-se saber se ele é «baixo» ou «alto» no contexto da distribuição F. Assim, para cálculos «à mão» importa considerar a localização da mediana das distribuições F rodam o valor 1. Por exemplo, um valor de 0.2 é um «valor baixo» e um valor de 3 ou 5 é um valor alto. A exata centralidade depende dos graus de liberdade.
Note-se, no seguinte gráfico, a posição das densidades em relação ao valor 1 no eixo do xx:
R Project
O comando pf com opção lower.tail=FALSE permite calcular \(P(F>10.675)\) com \(n=2\) e \(m=15\) graus de liberdade:
pf(10.675, df1=2, df2=15, lower.tail=FALSE)
[1] 0.001308885
Para saber a mediana,
qf(0.5, df1=2, df2=15)
Na página R: comandos online pode correr estes comandos para outros valores.
texas TI 84 e variantes
Pretende-se calcular \(P(F>10.675)\) com \(n=2\) e \(m=15\) graus de liberdade:
2nd => DISTR => 9:Fcdf => ENTER
Introduzir os valores dos parâmetros da Fisher para obter a probabilidade pretendida,
valor-p = \(P(F \geq 10.675 ) = Fcdf(10.675,10^{10}, 2, 15)\)
Excel
Por fazer.