teste e intervalo Z para a média 

Testes e intervalo de confiança para a média (\(\mu\)) de uma população normal com variância conhecida (\(\sigma^2\)). Em notação matemática:

\(X \sim N(\mu,\; \sigma^2)\): os dados são bem modelados por uma distribuição normal
\(\sigma^2\) é conhecida do problema em investigação (ver variância populacional)

e nestas condições, a variável fulcral é

\[Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \; \sim \; N(0,\; 1)\]

que segue distribuição de amostragem Normal.

procedimento para obter o IC 

Conhecida a média amostral (ver também medidas amostrais) o IC, com \(1-\alpha\) de confiança, é dado por

\[IC_{1-\alpha}(\mu) = \left] \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right[\]

em que, com base na distribuição normal padrão Z,

\[z_{1-\alpha/2} = \text{INV.Normal}(1-\alpha/2; 0; 1)\]

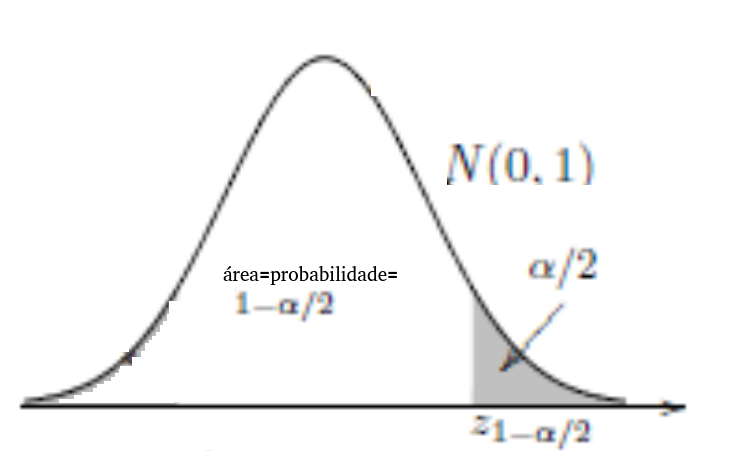
É mostrado, na figura, que o grau de confiança, \(1 - \alpha\), é colocado no centro da distribuição N(0, 1):

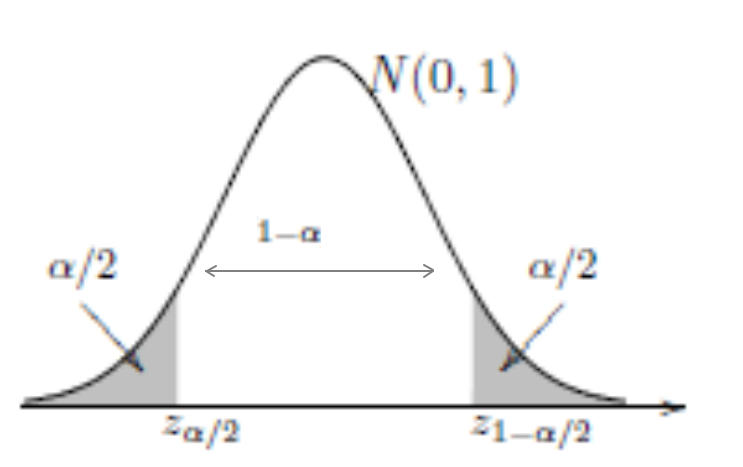
TH com base no p-value

Antes de avançar é necessária a verificação dos pressupostos:

\(X \sim N(\mu,\sigma^2)\) (X segue uma distribuição normal)
\(\sigma^2\) conhecido (a variância populacional é conhecida)

As etapas são:

1. Especificar a hipóteses H0 e H1: \(\mu_0\) é um valor real obtido no problema em investigação.

teste bilateral:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu \neq \mu_0\)
teste unilateral à direita:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu > \mu_0\)
teste unilateral à esquerda:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu < \mu_0\)

2. Identificar a estatística de teste: A notação «\(| \; H_0\)» designa «sob H0», ou seja, sendo H0 verdade então o valor do parâmetro \(\mu\) é o valor real \(\mu_0\) indicado no problema em investigação.

\[Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \; | \; H_0 \; \sim N(0,\;1)\]

3. Obter o valor da estatística de teste: Com base na média amostral e valor \(\mu_0\):

\[z_{obs} = \frac{\bar x - \mu_0}{\sigma/\sqrt{n}}\]

4. Calcular o p-value

Consideram-se os três casos.

No que se segue, \(\Phi(z) = \text{CDF.Normal}(z,\; 0,\; 1)\).

4a. Calcular o p-value de um teste bilateral

se \(z_{obs}\) é negativo então
- tabelas: \(\text{p-value} = 2 \times \Phi(z_{obs})\)
- calculadoras: \(\text{p-value} = 2 \times \text{CDF.Normal}(lower=-\infty,\;upper=z_{obs},\;\mu=0,\;\sigma=1)\)
se \(z_{obs}\) é positivo então
- tabelas: \(\text{p-value} = 2 \times (1 - \Phi(z_{obs}))\)
- calculadoras: \(\text{p-value} = 2 \times \text{CDF.Normal}(z_{obs},\;+\infty,\;0,\;1)\)

4b. Calcular o p-value de um teste unilateral à direita

Independentemente de \(z_{obs}\) ser positivo ou negativo:

tabelas: \(\text{p-value} = 1 - \Phi(z_{obs})\)

calculadoras: \(\text{p-value} = \text{CDF.Normal}(z_{obs},\;+\infty,\;0,\;1)\)

4c. Calcular o p-value de um teste unilateral à esquerda

Independentemente de \(z_{obs}\) ser positivo ou negativo:

tabelas: \(\text{p-value} = \Phi(z_{obs})\)

calculadoras: \(\text{p-value} = \text{CDF.Normal}(-\infty,\;z_{obs},\;\;0,\;1)\)

5. Concluir

se \(\text{p-value} \le \alpha\) então rejeita-se H0 em favor de H1
se \(\text{p-value} > \alpha\) então não se rejeita H0

4. Interpretar no contexto do problema em investigação.

Sugestão de interpretação (para o caso em que X é um peso):

«o peso médio (é / não é) significativamente diferente de \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«o peso médio (é / não é) significativamente maior que \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«o peso médio (é / não é) significativamente menor que \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

TH com base na região crítica 

Antes de avançar é necessária a verificação dos pressupostos:

\(X \sim N(\mu,\sigma^2)\) (X segue uma distribuição normal)
\(\sigma^2\) (a variância populacional é conhecida)

As etapas são:

1. Especificar a hipóteses H0 e H1: \(\mu_0\) é um valor real obtido no problema em investigação.

teste bilateral:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu \neq \mu_0\)
teste unilateral à direita:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu > \mu_0\)
teste unilateral à esquerda:
- \(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu < \mu_0\)

2. Identificar a estatística de teste: A notação «\(| \; H_0\)» designa «sob H0», ou seja, sendo H0 verdade então o valor do parâmetro \(\mu\) é o valor real \(\mu_0\) indicado no problema em investigação.

\[Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \; | \; H_0 \; \sim N(0,\;1)\]

3. Obter o valor da estatística de teste:: Com base na média amostral e valor \(\mu_0\).

\[z_{obs} = \frac{\bar x - \mu_0}{\sigma/\sqrt{n}}\]

No que se segue, \(\Phi(z) = \text{CDF.Normal}(z,\; 0,\; 1)\).

4. Obter a região crítica.: A região crítica é um intervalo onde se rejeita H0 caso este contenha \(z_{obs}\).

4a. região crítica bilateral

tabelas: \(z_{critico} = \Phi^{-1}(1-\alpha/2)\)
calculadoras: \(z_{critico} = \text{INV.Normal}(1-\alpha/2,\;0,\; 1)\) (o resultado é positivo)

\(RC = ]-\infty,\; z_{critico}[ \;\cup\; ]z_{critico},\; +\infty[\).

4b. região crítica unilateral à direita

tabelas: \(z_{critico} = \Phi^{-1}(1-\alpha)\)
calculadoras: \(z_{critico} =\text{INV.Normal}(1-\alpha,\;0,\; 1)\) (o resultado é positivo)

\(RC = ]z_{critico},\; +\infty[\)

4c. região crítica unilateral à esquerda

tabelas: \(z_{critico} = \Phi^{-1}(\alpha)\)
calculadoras: \(z_{critico} = \text{INV.Normal}(\alpha,\;0,\; 1)\) (o resultado é negativo)

\(RC = ]-\infty,\; z_{critico}[\)

5. Concluir.

se \(z_{obs}\) pertence à região crítica então rejeita-se H0 em favor de H1,
se \(z_{obs}\) não pertence à região crítica então não se rejeita H0.

4. Interpretar no contexto do problema em investigação.

Sugestão de interpretação (para o caso em que X é um peso):

«o peso médio (é / não é) significativamente diferente de \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«o peso médio (é / não é) significativamente maior que \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«o peso médio (é / não é) significativamente menor que \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

TH com base no método do IC 

Antes de avançar é necessária a verificação dos pressupostos:

\(X \sim N(\mu,\sigma^2)\) (X segue uma distribuição normal)
\(\sigma^2\) (a variância populacional é conhecida)
o TH a efetuar é do tipo bilateral (\(H_1:\; \mu \neq \mu_0\))

As etapas são:

1. Especificar a hipóteses H0 e H1: \(\mu_0\) é um valor real obtido no problema em investigação.

O método do IC apenas se aplica ao teste bilateral:

\(H_0:\, \mu = \mu_0 \quad vs \quad H_1:\, \mu \neq \mu_0\)

2. Usar ou determinar o IC: (ver também procedimento para obter o IC)

Se o problema em investigação já dispõe de um IC passa-se para a etapa seguinte.

O IC é obtido com grau de confiança \(1 - \alpha\)
O IC é dado por:

\[IC_{1-\alpha}(\mu) = \left] \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right[\]

3. Concluir

se \(\mu_0\) não pertence ao IC então rejeita-se H0 em favor de H1,
se \(\mu_0\) pertence ao IC então não se rejeita H0.

4. Interpretar no contexto do problema em investigação.

Sugestão de interpretação (para o caso em que X é um peso):

«o peso médio (é / não é) significativamente diferente de \(\mu_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

Recorda-se: o método do IC só é aplicável ao teste bilateral.