correlação de Pearson

O coeficiente de correlação de Pearson, r, aplica-se a duas variáveis numéricas emparelhadas $(x_i,y_i)$ e mede a correlação linear entre ambas.

Após a visualização do diagrama de dispersão pode usar-se o coeficiente para medir o grau de correlação e então:

se r=1 então os pontos $(x_i,y_i)$ definem pontos perfeitamente alinhados sobre um reta crescente;
se r=-1 então os pontos $(x_i,y_i)$ definem pontos perfeitamente alinhados sobre um reta decrescente;
se r=0 então os pontos $(x_i,y_i)$ não estão linearmente correlacionados

Consulte os exemplos ilucidativos na página wikipédia.

coeficiente amostral de Pearson

A amostra, de dimensão n, é constituída por pares de números reais $(x_i,y_i)$ em que $i=1, \ldots,n$ .

O coeficiente de Pearson, com base numa amostra, é determinado por

$r = \frac{ \sum_{i=1}^n (x_i - \bar x)(y_i - \bar y) }{ \sqrt{\sum_{i=1}^n (x_i - \bar x)^2} \sqrt{\sum_{i=1}^n (y_i - \bar y)^2} }$

A ideia, centrando a origem dos eixos em $(\bar x, \bar y)$ , pode ser facilmente reconhecida na imagem:

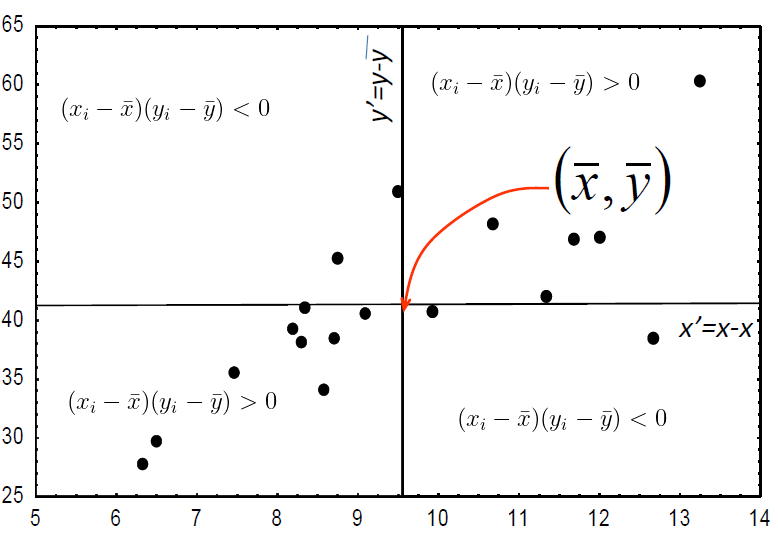
Repare-se que:

os pontos no primeiro e terceiro quadrantes registam um valor de $(x_i - \bar x)(y_i - \bar y)$ positivo;
os pontos no segundo e quarto quadrantes registam um valor de $(x_i - \bar x)(y_i - \bar y)$ negativo.

O sinal de r é determinado pelo numerador, pois o denominador de r é sempre positivo, e assim:

quando a larga maioria de pontos está no primeiro e terceiro quadrantes então $r > 0$ ;
quando a larga maioria de pontos está no segundo e quarto quadrantes então $r < 0$ ;
quando há pontos dispersos por todos os quadrantes então $\sum_{i=1}^n (x_i - \bar x)(y_i - \bar y)$ vai aproximar-se de 0 porque se estará a somar quantidades positivas e negativas.

teste ao coeficiente populacional de Pearson

Definindo $\rho$ como o coeficiente populacional de Pearson então pretende-se testar

$H0: \rho = 0 \text{ vs } H1: \rho \neq 0$

ou outra variante unilateral.

Sendo r o coeficiente amostral de Pearson, então a estatística de teste

$T|H0 = r \sqrt{ \frac{ n-2 }{ 1-r^2 } } \sim_{H0} t_{n-2}$

R project

x = c(36, 22, 25, 34, 26, 25, 23, 42, 25, 40, 35, 40)
y = c(54, 43, 47, 59, 54, 44, 46, 61, 51, 67, 64, 57)
plot(x,y)

cor.test(x,y, method="pearson")

calculadoras

comando: LinRegTTest

aspetos matemáticos

O coeficiente amostral de Pearson pode ser visto como a covariância amostral entre X e Y normalizada (o denominador faz a normalização e assim $-1 \le r \le 1$ ).

$r = \frac{ s_{XY} }{ s_X \times s_Y }$