inferência sobre proporções 

Testes e intervalo de confiança para uma proporção, \(p\) (parâmetro populacional), com recurso ao teorema do limite central considerando que

\(X_i,\, i=1,\ldots,n\) constituí uma amostra com valores 1 e 0 (1 indicando «sucesso» e 0 indicando «falha»);
\(n \ge 30\) (ver dimensão da amostra)
\(X=X_1 + \cdots + X_n\) é a soma total de sucessos:
- sendo uma soma de v.a. então pode aplicar-se o teorema do limite central

Um estimador para \(p\), a proporção populacional de sucessos, é dada por então

\[\hat p = \frac{X}{n},\]

em que \(X\) é o total de sucessos. A variável fulcral segue, aproximadamente, a distribuição normal padrão Z

\[Z = \frac{\hat p - p}{\sqrt{p(1-p)/n}} \; \sim_{aprox} \; N(0,\; 1)\]

procedimento para obter o IC 

Conhecida a proporção amostral de sucessos, ou estimativa para \(p\),

\[\hat p = \frac{x}{n},\]

fixado o grau de confiança \(1-\alpha\), pressupondo \(n \ge 30\), então uma aproximação do IC para uma proporção é dada por

\[IC_{1-\alpha}(p) \approx \left[ \hat p - z_{1-\alpha/2} \sqrt{\hat p (1-\hat p)/n},\; \hat p + z_{1-\alpha/2} \sqrt{\hat p (1-\hat p)/n} \right]\]

em que, com base na distribuição normal padrão Z,

\[z_{1-\alpha/2} = \text{INV.Normal}(1-\alpha/2; 0; 1)\]

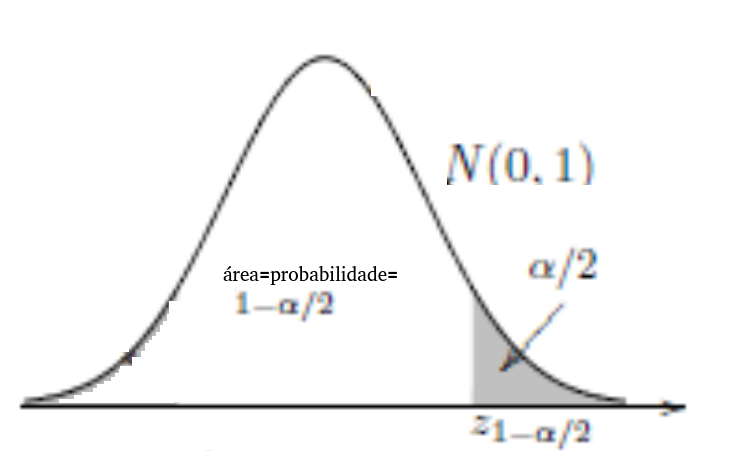
É mostrado, na figura, que o grau de confiança, \(1 - \alpha\), é colocado no centro da distribuição N(0, 1):

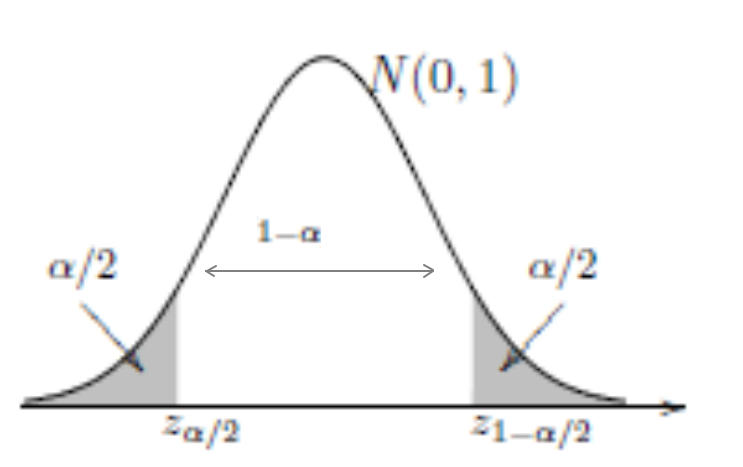
TH com base no p-value

Antes de avançar é necessária a verificação dos pressupostos:

\(n \ge 30\) (a amostra é suficientemente grande para se usar a aproximação pelo TLC)

considerando que:

\(X_i=0\) indica «insucesso» na obseração i (ver distribuição de Bernoulli)
\(X_i=1\) indica «sucesso» na obseração i
\(X=X_1+\cdots+X_n\) é a soma de sucessos/insucessos que justifica o uso do TLC
\(p\) é a proporção populacional de sucessos
\(\hat p=x/n\) é a proporção estimada de sucessos

1. Especificar a hipóteses H0 e H1 em que: \(p\) é a proporção de indivíduos com uma dada característica na população (parâmetro desconhecido) e \(p_0\) é uma proporção indicada no problema em investigação:

teste bilateral:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p \neq p_0\)
teste unilateral à direita:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p > p_0\)
teste unilateral à esquerda:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p < p_0\)

2. Identificar a estatística de teste para os pressupostos dados:: Pressupondo \(n \ge 30\):

\[Z = \frac{\hat p - p}{\sqrt{p(1-p)/n}} \; | \; H_0 \; \sim_{aprox} N(0,\;1)\]

sendo \(\hat p = \frac{X}{n}\) o estimador da proporção populacional p.

3. Obter o valor da estatística de teste

o valor \(p_0\) é fornecido em H0;
\(\hat p = \frac{x}{n}\) é a estimativa da proporção p.

\[z_{obs} = \frac{\hat p - p_0}{\sqrt{p_0(1-p_0)/n}}\]

em que \(p_0\) é o valor de p assumido em H0.

4. Calcular o p-value

Consideram-se os três casos.

No que se segue, \(\Phi(z) = \text{CDF.Normal}(z,\; 0,\; 1)\).

4a. Calcular o p-value de um teste bilateral

se \(z_{obs}\) é negativo então
- tabelas: \(\text{p-value} = 2 \times \Phi(z_{obs})\)
- calculadoras: \(\text{p-value} = 2 \times \text{CDF.Normal}(-\infty,\;z_{obs},\; 0,\; 1)\)
se \(z_{obs}\) é positivo então
- tabelas: \(\text{p-value} = 2 \times (1 - \Phi(z_{obs}))\)
- calculadoras: \(\text{p-value} = 2 \times \text{CDF.Normal}(z_{obs},\;+\infty,\; 0,\; 1)\)

4b. Calcular o p-value de um teste unilateral à direita

Independentemente de \(z_{obs}\) ser positivo ou negativo interessa só a probabilidade à direita de \(z_{obs}\):

tabelas: \(\text{p-value} = 1 - \Phi(z_{obs})\)

calculadoras: \(\text{p-value} = \text{CDF.Normal}(z_{obs},\;+\infty,\; 0,\; 1)\)

4c. Calcular o p-value de um teste unilateral à esquerda

Independentemente de \(z_{obs}\) ser positivo ou negativo interessa só a probabilidade à esquerda de \(z_{obs}\):

tabelas: \(\text{p-value} = \Phi(z_{obs})\)

calculadoras: \(\text{p-value} = \text{CDF.Normal}(-\infty,\; z_{obs},\; 0,\; 1)\)

calculadora gráfica: verifique o resultado efetuando o cálculo do p-value com as funções de teste de hipóteses.

5. Concluir

se \(\text{p-value} \le \alpha\) então rejeita-se H0 em favor de H1
se \(\text{p-value} > \alpha\) então não se rejeita H0

6. Interpretar no contexto do problema em investigação:

Sugestão de interpretação:

«a proporção de indivíduos com dada característica (é / não é) significativamente diferente que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«a proporção de indivíduos com dada característica (é / não é) significativamente maior que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«a proporção de indivíduos com dada característica (é / não é) significativamente menor que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

TH com base na região crítica 

Antes de avançar é necessária a verificação dos pressupostos:

\(n \ge 30\) (a amostra é suficientemente grande para se usar a aproximação pelo TLC)

considerando que:

\(X_i=0\) indica «insucesso» na obseração i (ver distribuição de Bernoulli)
\(X_i=1\) indica «sucesso» na obseração i
\(X=X_1+\cdots+X_n\) é a soma de sucessos/insucessos que justifica o uso do TLC
\(p\) é a proporção populacional de sucessos
\(\hat p=x/n\) é a proporção estimada de sucessos

1. Especificar a hipóteses H0 e H1.: \(p\) é a proporção de indivíduos com uma dada característica na população (parâmetro desconhecido) e \(p_0\) é uma proporção indicada no problema em investigação:

teste bilateral:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p \neq p_0\)
teste unilateral à direita:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p > p_0\)
teste unilateral à esquerda:
- \(H_0:\; p = p_0 \quad vs \quad H_1:\; p < p_0\)

2. Identificar a estatística de teste.: Pressupondo \(n \ge 30\):

\[Z = \frac{\hat p - p}{\sqrt{p(1-p)/n}} \; | \; H_0 \; \sim_{aprox} N(0,\;1)\]

com \(\hat p = \frac{X}{n}\).

3. Obter o valor da estatística de teste

o valor \(p_0\) é fornecido em H0;
\(\hat p = \frac{x}{n}\) é a estimativa da proporção p.

\[z_{obs} = \frac{\hat p - p_0}{\sqrt{p_0(1-p_0)/n}}\]

4. Obter a região crítica.: A região crítica é um intervalo onde se rejeita H0 caso este contenha \(z_{obs}\).

4a. região crítica bilateral

tabelas: \(z_{critico} = \Phi^{-1}(1-\alpha/2)\)
calculadoras: \(z_{critico} = \text{INV.Normal}(1-\alpha/2,\;0,\; 1)\) (o resultado é positivo)

\(RC = ]-\infty,\; z_{critico}[ \;\cup\; ]z_{critico},\; +\infty[\).

4b. região crítica unilateral à direita

tabelas: \(z_{critico} = \Phi^{-1}(1-\alpha)\)
calculadoras: \(z_{critico} =\text{INV.Normal}(1-\alpha,\;0,\; 1)\) (o resultado é positivo)

\(RC = ]z_{critico},\; +\infty[\)

4c. região crítica unilateral à esquerda

tabelas: \(z_{critico} = \Phi^{-1}(\alpha)\)
calculadoras: \(z_{critico} = \text{INV.Normal}(\alpha,\;0,\; 1)\) (o resultado é negativo)

\(RC = ]-\infty,\; z_{critico}[\)

Nota: as calculadoras, em geral, não determinam a região crítica.

5. Concluir.

se \(z_{obs}\) pertence à região crítica então rejeita-se H0 em favor de H1,
se \(z_{obs}\) não pertence à região crítica então não se rejeita H0.

6. Interpretar no contexto do problema em investigação.

Sugestão de interpretação:

«a proporção de indivíduos com dada característica (é / não é) significativamente diferente que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«a proporção de indivíduos com dada característica (é / não é) significativamente maior que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»
«a proporção de indivíduos com dada característica (é / não é) significativamente menor que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

TH com base no método do IC 

Antes de avançar é necessária a verificação dos pressupostos:

\(n \ge 30\) (a amostra é suficientemente grande para se usar a aproximação pelo TLC)
o TH a efetuar é do tipo bilateral (\(H_1:\; p \neq p_0\))

considerando que:

\(X_i=0\) indica «insucesso» na obseração i (ver distribuição de Bernoulli)
\(X_i=1\) indica «sucesso» na obseração i
\(X=X_1+\cdots+X_n\) é a soma de sucessos/insucessos que justifica o uso do TLC
\(p\) é a proporção populacional de sucessos
\(\hat p=x/n\) é a proporção estimada de sucessos

1. Especificar a hipóteses H0 e H1 em que: \(p\) é a proporção de indivíduos com uma dada característica na população (parâmetro desconhecido) e \(p_0\) é uma proporção indicada no problema em investigação.

O método do IC apenas se aplica ao teste bilateral:

\(H_0:\; p = p_0 \quad vs \quad H_1:\; p \neq p_0\)

2. Usar ou determinar o IC (ver procedimento para obter o IC).

Se o problema em investigação já dispõe de um IC passa-se para a etapa seguinte.

Com

o pressuposto de \(n \ge 30\)
o grau de confiança é \(1 - \alpha\)

então o IC aproximado é dado por

\[IC_{1-\alpha}(p) \approx \left[ \hat p - z_{1-\alpha/2} \sqrt{\hat p (1-\hat p)/n},\; \hat p + z_{1-\alpha/2} \sqrt{\hat p (1-\hat p)/n} \right]\]

3. Concluir

se \(p_0\) não pertence ao IC então rejeita-se H0 em favor de H1,
se \(p_0\) pertence ao IC então não se rejeita H0.

4. Interpretar no contexto do problema em investigação:

Sugestão de interpretação:

«a proporção de indivíduos com dada característica (é / não é) significativamente diferente que \(p_0\) considerando o nível de significância \(\alpha=5\%\) e com base na amostra considerada.»

(Recorda-se: O método do IC só é aplicável para hipóteses bilaterais.)

outras designações do teste à proporção 

Testes em populações de Bernoulli
Teste assintótico para uma proporção p

pressupostos mais exigentes 

Os método de inferência usados para a proporção, nesta página, fornecem soluções aproximadas. Por forma a melhorar a aproximação podem ser adicionados mais pressupostos: