correlação, gráfico de dispersão e causalidade

Uma relação, na matemática, é um par \((a,b)\) entre dois elementos de dois conjuntos, não vazios, A e B.

O termo correlação encontra-se na literatura como sendo uma medida do emparelhamento entre pares de números indicando que conhecendo uma concretização x de variável aleatória X se pode saber, sujeito a erro, uma concretização possível y, de uma variável aleatória Y. O termo correlação inclui, em geral na literatura, as naturais variações dos fenómenos universais.

etapas

As etapas do estudo de correlação são:

Construir o diagrama de dispersão.
Calcular as medidas de correlação apropriadas.
Realizar um teste de hipóteses quantificando se o coeficiente populacional é ou não significativo.
Averiguar se existe causalidade (sendo este tema totalmente dependente do contexto científico do estudo).

diagrama de dispersão

É sempre importante preceder o uso dos coeficientes com o diagrama de dispersão que ajuda a perceber qual o coeficiente mais indicado. A figura mostra três casos abordados neste texto:

Nesta primeira imagem, o valor aproximado de x determina o valor aproximado de y, e percebe-se uma correlação linear.

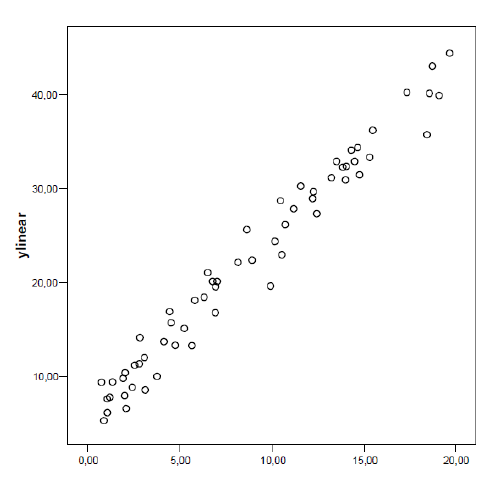
Nesta segunda imagem, o valor aproximado de x determina o valor aproximado de y, e percebe-se uma correlação não linear;

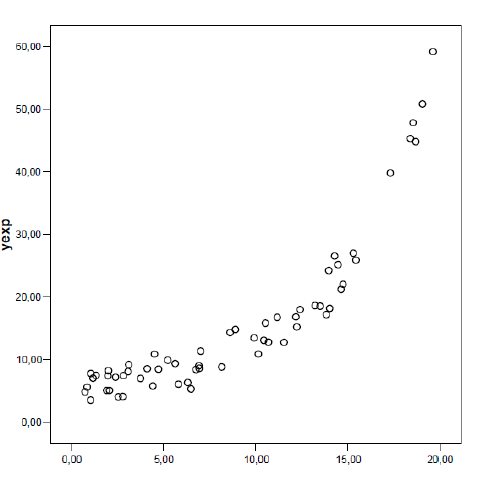
Nesta terceira imagem, o valor aproximado de x não determina o valor aproximado de y: conhecendo um valor em x não se pode inferir se o valor em y será elevado ou baixo.

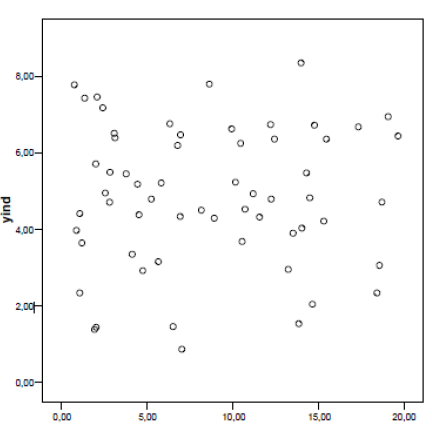
medidas de correlação e seus testes

As conclusões visuais obtidas por gráficos carecem de medidas quantitativas e testes de hipóteses.

São considerados os seguintes casos de correlação entre duas variáveis aleatórias X e Y:

a correlação linear, com normalidade das variáveis X e Y, é medida pelo correlação de Pearson;
a correlação linear, sem normalidade, das variáveis X e Y, é medida pelo correlação de Spearman;
a correlação monónota, não necessariamente linear, é medida pelo correlação de Spearman;
a ausência de correlação, isto é, independência entre X e Y, é medida com ambos os coeficientes.

(Outras situações não são aqui exploradas.)

causalidade

Correlação não quer dizer que exista causalidade existindo inúmeros, talvez divertidos (mas também perigosos), exemplos de boa correlação sem qualquer nexo de causalidade. Muitas vezes, a explicação de tal correlação entre variáveis, está no contexto e não na causalidade.

O exemplo comum de ilusão de causalidade é quando há um fator comum. Por exemplo, o tempo. O número de copos de água bebidos pelo leitor tem aumentado desde que nasceu assim como o número de golos da sua equipe favorita também tem aumentado. Difícil será explicar que ao beber água se esteja a causar mais golos. O fator comum é o tempo: quando mais tempo mais copos de água, quanto mais tempo mais golos são marcados.

Já o CO2 excessivo está a causar o aumento da temperatura média global (embora de forma diferente de zona para zona do planeta). Esta relação de causalidade precisou de muitos estudos até ser aceite globalmente pela comunidade científica.