função de distribuição empírica
Com base na tabela de frequências relativas acumuladas pode construir-se a função de distribuição empírica (no software é usado «cumulative») definida assim:
tendo a amostra dimensão n.
A função \(F_n(x)\) é construída com base numa amostra. Por isso não se diz que seja uma função que determina probabilidades mas antes a proporção de valores iguais ou inferiores a um dado x.
Exercise (1)
Se uma amostra é 0, 0, 0, 1, 2:
(a) qual a proporção de 0?
☞ proposta de resolução
Existem três zeros em cinco elementos da amostra. Assim 3/5 = 60%.
(b) qual o valor de \(F_5(1)\)?
☞ proposta de resolução
Existem 4 valores iguais ou inferiores a 1 e assim \(F_5(1)\) = 4/5 = 80%.
(c) porque é que uma função de distribuição empírica não calcula probabilidades?
☞ proposta de resolução
As função de distribuição determinam probabilidades porque respondem por toda a população.
A função de distribuição empírica responde apenas por uma amostra porque é construída para essa amostra; ao depender de cada amostra não se pode determinar probabilidades sobre a população.
exemplo
Considere a amostra composta por 75 zeros, 15 uns, 8 dois, e 2 três. O gráfico seguinte mostra a função \(F_n(x)\):
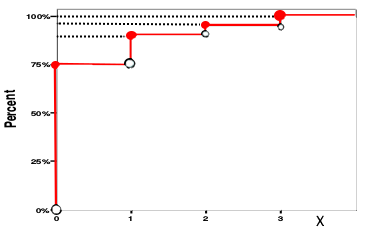
Exercise (2)
(a) O que é o n em \(F_n(x)\) ?
☞ proposta de resolução
O n é a dimensão da amostra: n=100 (=75+15+8+2).
(b) Determine o valor de \(F_n(1)\) e \(F_n(1.5)\).
☞ proposta de resolução
\(F_n(1)\) e \(F_n(1.5)\) tem o valor 90%.
(c) Qual a proporção de valores iguais ou inferiores a 1.5?
☞ proposta de resolução
Como \(F_n(1.5)=90\%\) então a proporção de valores iguais ou inferiores a 1.5 é 90%.
exercícios recomendados
☞ ex. 1.26 (*).