mediana amostral
A mediana é um valor que ocupa a posição central na amostra ordenada. Assim pode-se dizer, de forma incompleta mas facilmente memorizável, que
A mediana é um valor real e denota-se por \(m_e\).
exemplos
Se a amostra tiver
dimensão ímpar: a mediana, \(m_e\), coincide com a observação central
na amostra 1.2; 2.1; 2.1; 2.2; 2.4 a mediana é o valor 2.1.
dimensão par, a mediana toma o valor da média das duas observações mais centrais.
na amostra 0.0; 0.7; 0.9; 1.6 a mediana é o valor 0.8 resultado de (0.7+0.9)/2.
Nota: existem outras definições de mediana.
como calcular
Primeiro, ordena-se a amostra.
A mediana é obtida pela expressão matemática:
em que é bem clara a importância da posição central da amostra em \(n/2\).
Consideram-se dois casos: dados não agrupados e dados agrupados.
dados não agrupados
Com amostra de dimensão ímpar, a mediana, \(m_e\), coincide com a observação central
na amostra 1.2; 2.1; 2.1; 2.2; 2.4 a mediana é o valor 2.1.
mas para uma amostra maior pode ser útil seguir o seguinte detalhe rigoroso:
\(n=5\), então n é ímpar, e assim aplica-se \(x_{ ( \lfloor n/2 + 1 \rfloor ) }\)
\(n/2 = 2.5\), então \(n/2 + 1 = 3.5\). Assim \(\lfloor n/2 + 1 \rfloor = \lfloor 3.5 \rfloor = 3\)
a posição, na amostra ordenada, é a 3 e amostra ordenada, usando a notação rigorosa, é dada por
\(x_{(1)}=1.2\), \(x_{(2)}=2.1\), \(x_{(3)}=2.1\), \(x_{(4)}=2.2\), \(x_{(5)}=2.4\)
Assim, \(m_e = 2.1\)
Com amostra de dimensão par, a mediana toma o valor da média das duas observações mais centrais.
na amostra 0.0; 0.7; 0.9; 1.6 a mediana é o valor 0.8 resultado de (0.7+0.9)/2.
mas para uma amostra maior pode ser útil seguir o seguinte detalhe rigoroso:
\(n=4\), então n é par, e assim aplica-se \(\frac{ x_{(n/2)} + x_{(n/2+1)} }{2}\)
como \(n/2 = 2\) então \(m_e = (x_{(2)} + x_{(3)})/2\)
usando a notação rigorosa para amostras ordenadas:
\(x_{(1)}=0.0\), \(x_{(2)}=0.7\), \(x_{(3)}=0.9\), \(x_{(4)}=1.6\)
assim, \(m_e = (0.7+0.9)/2 = 0.8\)
dados agrupados
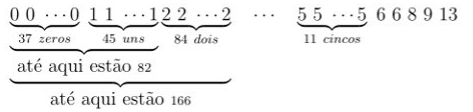
Considere-se uma amostra de dimensão \(n=257\) de dados agrupados
observações: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
13 |
que se repetem: |
37 |
45 |
84 |
52 |
23 |
11 |
2 |
1 |
1 |
1 |
Sendo n ímpar,
\(n/2 = 128.5\), então \(n/2 + 1 = 129.5\). Assim \(\lfloor n/2 + 1 \rfloor = \lfloor 129.53.5 \rfloor = 129\)
\(m_e = x_{(129)}\)
Para obter a posição 129 podemos acumular as ocorrências:
definição matemática rigorosa
Dizer que \(m_e\) é a mediana de uma amostra significa que pelo menos 50% dos dados são inferiores ou iguais a \(m_e\) e pelo menos 50% dos dados são superiores ou iguais a \(m_e\).
Comentários:
Desta definição resulta que pode existir um só valor mediano ou uma infinidade de soluções.
Na amostra 1, 2, 3, 4:
2 é uma mediana pois 50% das observações são iguais ou inferiores a 2 e pelo menos 50% são iguais ou superiores a 2
2.5 é uma mediana pois 50% das observações são iguais ou inferiores a 2.5 e 50% são iguais ou superiores a 2.5
3 é uma mediana pois pelo menos 50% das observações são iguais ou inferiores a 3 e 50% são iguais ou superiores a 3
Na amostra 1, 2, 3, 4, 5 só existe um valor mediano:
3 é uma mediana pois pelo menos 50% das observações são iguais ou inferiores a 3 e pelo menos 50% são iguais ou superiores a 3
calculadora gráfica
Para obter a mediana amostral e outras medidas consulte as medidas amostrais.
avançado
A mediana é mais robusta que a média a erros ou a observações afastadas.