quartil amostral

Na linguagem corrente não rigorosa diz-se que

• o primeiro quartil, que designa por $Q_1$, é um valor tal que:

  • pelo menos 25% das observações são iguais ou inferiores ao valor $Q_1$.

Usando o necessário rigor matemático, a frase acima está incompleta sendo necessário definir o valor $Q_1$ do seguinte modo.

• O primeiro quartil ($Q_1$) é um valor que obedece à conjunção de duas partes:

  • pelo menos 25% das observações são iguais ou inferiores ao valor $Q_1$ e

  • pelo menos 75% das observações são iguais ou superiores ao valor $Q_1$.

Por exemplo, na amostra ordenada (1, 2, 3, 4) pode escolher-se o valor $Q_1=2$ pois

• 2/4 = 50% (verifica o «pelo menos 25%») são iguais ou inferiores a Q1=2 e também

• 3/4= 75% (verifica o «pelo menos 75%») são iguais ou superiores a Q1=2

Agora vamos escolher $Q_1=4$ com a mesma amostra, (1, 2, 3, 4). Se a única permissa for «pelo menos 25% das observações são iguais ou inferiores ao valor $Q_1$» teríamos

• $Q_1=4$, i.e., 4/4 = 100% (verifica o «pelo menos 25%») das observações são iguais ou inferiores a Q1=4.

mas fará sentido «intuitivo» dizer que Q1=4 para a amostra (1, 2, 3, 4)? Não faz pois não transmite corretamente a ideia de um valor associado a 25% da amostra. Por isso é necessária a conjugação de duas partes, que agora se repetem:

• pelo menos 25% das observações são iguais ou inferiores ao valor $Q_1$ e

• pelo menos 75% das observações são iguais ou superiores ao valor $Q_1$.

Assim,

primeiro quartil ($Q_1$): pelo menos 25% das observações são iguais ou inferiores ao valor $Q_1$ e pelo menos 75% das observações são iguais ou superiores ao valor $Q_1$.

segundo quartil (ou mediana) ($Q_2$): pelo menos 50% das observações são iguais ou inferiores ao valor $Q_2$ e pelo menos 50% das observações são iguais ou superiores ao valor $Q_1$.

terceiro quartil ($Q_3$): pelo menos 75% das observações são iguais ou inferiores ao valor $Q_3$ e pelo menos 25% das observações são iguais ou superiores ao valor $Q_3$.

A imagem não abrange os casos todos pois os quartis podem coincidir em valor ficando sobrepostos:

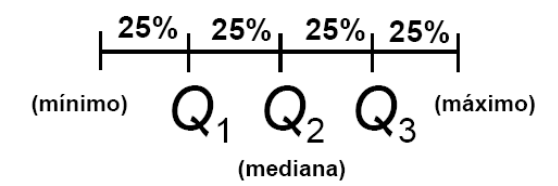
cálculo de quartis

O cálculo de quartis segue a expressão geral em quantil amostral, que se resume em:

• para $Q_1$, tem-se $p=0.25$;

• para $Q_2$, tem-se $p=0.50$;

• para $Q_3$, tem-se $p=0.75$.

Sendo n a dimensão da amostra:

• se $np$ não é inteiro, escolhe-se o inteiro seguinte, sem arredondar, para posição na amostra ordenada:

$$x_{\left( \lfloor np+1 \rfloor \right)}$$

• se $np$ é inteiro, faz-se média entre os dois valores consecutivos na amostra ordenada:

$$\frac{x_{(np)} + x_{(np+1)}}{2}$$

Aviso

O método de cálculo, acima, é uma simplificação de métodos mais ponderados usados em software. Assim, os quartis obtidos por software podem ser valores um pouco diferentes.

Consulte, também, quantil amostral.

máquina de calcular

Para obter a média e outras medidas use estes comandos:

R Project

A função summary() determina os quartis:

dados = c(0, 1, 1, 1, 1, 1, 1, 1, 1, 2)
summary(dados)

obtendo-se

Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
   0       1       1       1       1       2

A função quantile() calcula um qualquer quantil:

dados = c(0, 1, 1, 1, 1, 1, 1, 1, 1, 2)
quantile(dados, 0.25)

obtendo-se

25%
  1

ver também

• Os quartis são usados no desenho de um caixa de bigodes (boxplot).