ex. 1.26 (*)
Considere a amostra: 1.0, 1.0, 2.1, 4.1, 5.0, 6.0.
(a) Determine valores da função de distribuição empírica \(F_n(x)\) para cada elemento da amostra.
☞ proposta de resolução
A amostra tem dimensão 6. De modo sumariado, a função de distribuição empírica pode ter este aspeto:
para \(x = 1.0\) então \(F_6(1.0)=2/6 \approx 0.33\) (33% das observações da amostra são iguais ou menores que 1)
para \(x = 2.1\) então \(F_6(2.1)=3/6 = 0.5\) (50% das observações da amostra são iguais ou menores que 2.1)
para \(x = 4.1\) então \(F_6(4.1)=4/6 \approx 0.66\) (66% das observações da amostra são iguais ou menores que 4.1)
para \(x = 5.0\) então \(F_6(5.0)=5/6 \approx 0.83\) (83% das observações da amostra são iguais ou menores que 5)
para \(x = 6.0\) então \(F_6(6.0)=1\) (100% das observações são iguais ou inferiores a 6)
(b) Determine os seguintes valores da função de distribuição empírica: \(F_6(0)\), \(F_6(2.5)\) e \(F_6(7)\).
☞ proposta de resolução
A amostra tem dimensão 6.
\(F_6(0)=0\) pois 0 valores na amostra são iguais ou inferiores a 0.
\(F_6(2.5)=3/6=0.5\) pois 3 valores na amostra são iguais ou inferiores a 2.5.
\(F_6(7)\) pois todos os valores na amostra são iguais ou inferiores a 7.
A próxima alínea generaliza esta noção.
(c) Determine a função de distribuição empírica \(F_n(x)\).
☞ proposta de resolução
A função deve ser definida para qualquer valor no eixo xx: \(\mathbb{R}\).
Começa-se por definir os intervalos, em geral abertos à direita \([a,b[\):
\(x < 1\) - de \(-\infty\) até antes do primeiro valor observado;
\(1 \le x < 2.1\) - do 1º valor observado e ao 2º valor observado (aberto);
\(2.1 \le x < 4.1\) - do 2º valor observado e ao 3º valor observado (aberto);
\(4.1 \le x < 5\) - etc
\(5 \le x \le 6\) - etc
\(x \ge 6\) - do último valor observado até \(+\infty\)
Com rigor matemático, esta função escreve-se assim:
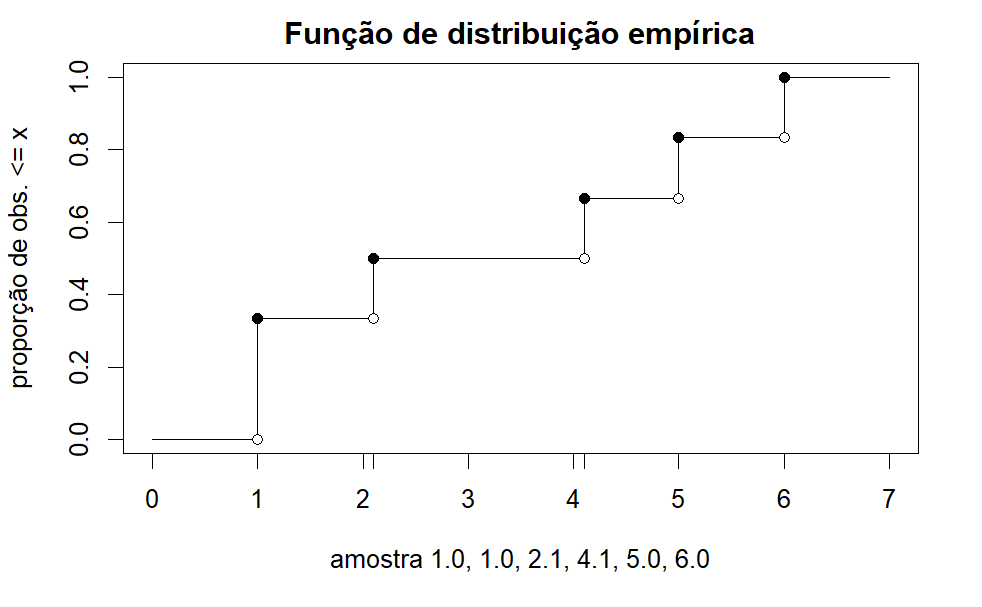
(d) Esboce o respetivo gráfico.
☞ proposta de resolução
(e) Use o gráfico, ou a função F, para calcular a proporção de elementos da amostra iguais ou inferiores a 1.5 e 4.5?
☞ proposta de resolução
x=1.5 está no intervalo \(1 \le x < 2.1\) e então F(1.5)=0.33;
x=4.5 está no intervalo \(4.1 \le x < 5\) e então F(4.5)=0.66.