caixa de bigodes (boxplot)
A caixa de bigodes, ou boxplot, corresponde a uma representação gráfica de quartis e, possivelmente, de alguns valores da amostra.
As caixas de bigodes fornecem informação visual sobre as seguintes medidas amostrais:
Localização central: mediana amostral (\(m_e\) ou \(Q_2\))
Localizações relativas: 1º e 3º quartis, mínimo e máximo (\(Q_1\) e \(Q_3\)).
Dispersão: amplitude (máximo - mínimo) e distância interquartil (\(H=Q_3 - Q_1\)).
Assimetria: posição relativa dos quartis, o comprimento dos bigodes e a existência de valores atípicos.
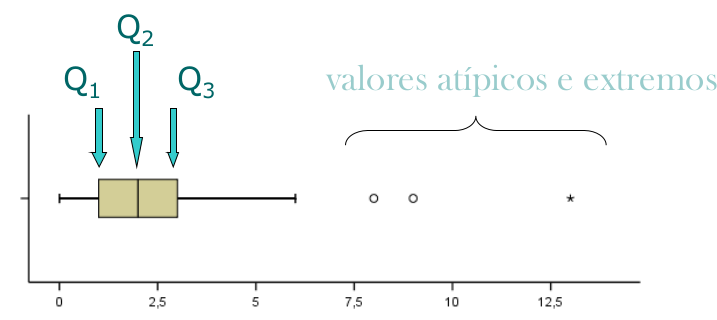
caixa de bigodes comparativas
As caixas de bigodes também são úteis para comparar várias amostras num mesmo gráfico, caixas de bigodes comparativas.
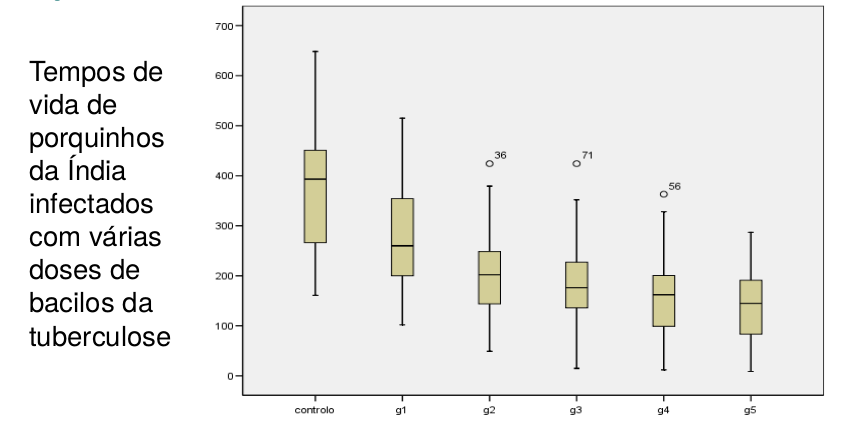
exemplo
Observações a azul:
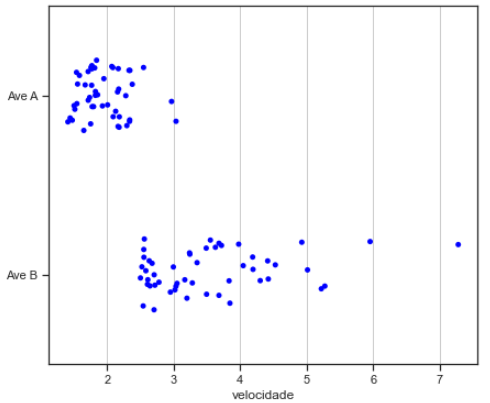
Caixa de bigodes:
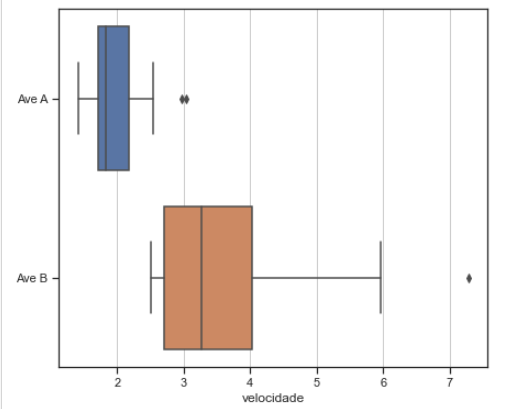
Sobreposição da amostra (azul) e as caixas de bigodes:
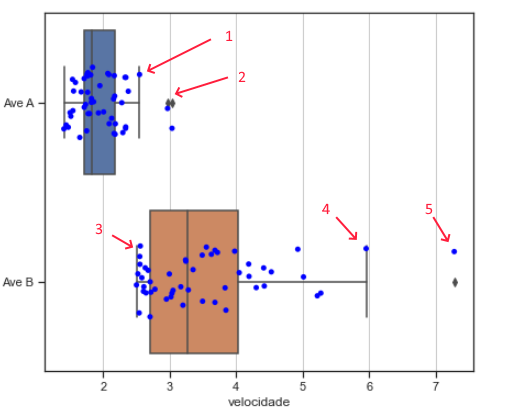
1: o «bigode» superior vai até ao valor observado (marcado a azul);
2: na zona «2» ocorrem dois valores atípicos: as observações estão marcadas a azul e o losangos pertencem à caixa-de-bigodes e desigan-se por valores atípicos;
3: há uma observação azul que marca o bigode, e as outras, ainda que próximas, não ultrapassam o «bigode inferior»; caso contrário seriam valores atípicos;
4: um valor observado marca a posição do bigode superior;
5: um valor atípico (azul é o observado e o losango pertence ao desenho da caixa de bigodes).
construir uma caixa-de-bigodes
Para construir um boxplot seguindo todas as etapas. Vamos usar as noções:
localização central: mediana amostral (\(m_e\) ou \(Q_2\));
localizações relativas: 1º e 3º quartis (\(Q_1\) e \(Q_3\)), mínimo e máximo.
As etapas de arranque são:
Ordenar a amostra.
Obter \(Q_1\), \(Q_2\), \(Q_3\) (ver quartil amostral)
Obter \(H=Q_3 - Q_1\) (amplitude interquartil amostral)
Calcular as barreiras:
\(Q_1 - 3H\) (barreira de valores atípicos severos inferiores)
\(Q_1 - 1.5H\) (barreira de valores atípicos moderados inferiores)
\(Q_3 + 1.5H\) (barreira de valores atípicos moderados superiores)
\(Q_3 + 3H\) (barreira de valores atípicos severos superiores)
Traçar a caixa-de-bigodes:
Traçar o corpo central da caixa usando \(Q_1\), \(Q_2\), \(Q_3\); a mediana é esboçada com traço mais espesso.
Marcar apenas as barreiras que estão contidas entre o mínimo e máximo da amostra; pode usar-se traço interronpido pois estas barreiras não fazem parte da caixa.
Marcar valores atípicos moderados com o símbolo «o».
Marcar valores atípicos severos com o símbolo «*» .
Questões frequentes
O bigode vai até à barreira moderada? Um bigode pode ir até à barreira moderada se existir algum valor na amostra que coincida com a barreira. Em geral, o bigode pára num valor que esteja na amostra (ordenada) e não chega à barreira, isto é, a observação está antes da barreira.
Os valores atípicos podem ser marcados na barreira? Sim, se existir um valor atípico moderado na amostra e que coincida com a barreira de valores severos então o valor atípico moderado pode ser marcado com o símbolo «o» por forma a coincidir com a barreira; os restantes valores atípicos já serão marcados com asteriscos «*».
Por fazer
exemplos de boxplots para acabar o tutorial
R Project
Seguem exemplos de construção em R :
alturas = c(18.3, 20.9, 22.0, 20.3, 18.0, 18.6, 20.9, 17.9, 20.2, 18.0, 28.0)
boxplot(alturas) #os valores atípicos são marcados apenas com 'o'
Caixa-de-bigodes comparativas:
norte = c(18.1, 21.4, 22.7, 17.9, 18.5, 18.7, 19.5, 23.7, 25.2, 18.1)
sul = c(10.2, 11.6, 11.4, 9.7, 9.1, 9.1, 10.7, 13.2, 11.5, 8.7)
dados = data.frame(norte=norte, sul=sul)
boxplot(dados)