teste de hipóteses 

Um teste de hipóteses (TH) envolve:

a confrontação de duas hipóteses, designadas por H0 e H1
a hipótese sob investigação é a H1, também designada por Ha de «hipótese alternativa».
um método para realizar o TH;
verificação de pressupostos que permitem a realização do TH.

Exemplo:

H0: um dado tratamento, em média, produz resultados padronizados;
H1: um dado tratamento, em média, produz melhores resultados;

tipos de hipóteses 

Consideremos uma população normal para a qual desejamos efetuar um teste de hipóteses sobre a média populacional, \(\mu\). São possíveis três casos, nos quais se usa o valor 23 como exemplo, neste tutorial:

teste bilateral:

\[H_0\,:\, \mu = 23 \quad vs \quad H_1\,:\, \mu \neq 23\]

teste unilateral à direita:

\[H_0\,:\, \mu = 23 \quad vs \quad H_1\,:\, \mu > 23\]

teste unilateral à esquerda:

\[H_0\,:\, \mu = 23 \quad vs \quad H_1\,:\, \mu < 23\]

erros inerentes e decisão 

Na tomada de decisão entre as duas hipóteses, H0 e H1, surgem duas possibilidades de erro, designadas por erro de tipo I e erro de tipo II:

	H0 é verdadeira	H1 é verdadeira
Rejeito H0	erro de tipo I	decisão acertada
Não rejeito H0	decisão acertada	erro de tipo II

O erro de tipo I ocorre quando: se rejeita H0 sendo H0 a hipótese verdadeira.
O erro de tipo II ocorre quando: não se rejeita H0 sendo H1 a hipótese verdadeira.

Nota: «sendo que» é o mesmo que «dado que».

Para tomar uma decisão em contexto de incerteza é necessário fixar uma probabilidade de se cometerem esses erros. O método usual é fixar o valor de probabilidade do erro «rejeitar H0 dado que H0 é verdade» num valor baixo, como 5%. Da seguinte expressão obtém-se regras para tomar uma decisão:

\[\begin{split}\begin{eqnarray*} \alpha & = & P(\text{cometer erro de tipo I}) \\ & = & P(\text{rejeitar }H_0\,|\, H_0\text{ é verdadeira}) \\ & = & P(\text{Com uma Amostra Aleatória rejeitar }H_0\,|\, H_0\text{ é verdadeira}) \end{eqnarray*}\end{split}\]

O valor \(\alpha\) designa-se por nível de significância do teste. Os níveis usuais de significância são \(\alpha=5\%\) ou ainda 1%, 10%. Podem ser mais pequenos, por exemplo na indústria farmacêutica.

um enunciado ilustrativo 

Para introduzir os três métodos que permitem a realização de um teste de hipóteses considera-se a motivação nascida da situação concreta neste enunciado.

O índice de massa corporal médio de uma população, \(\mu\), pode ser um sinal de aviso para se implementarem políticas anti-obesidade. A questão anterior pode ser traduzida no confrontro de duas hipóteses,

um neutra, H0, que indica que em termos médios a população não está obesa
e uma hipótese sob investigação, H1 (ou hipótese alternativa): que sugere que, em termos médios, a população está obesa.

A formalização, para valores padrão do IMC, pode ser esta:

\[H_0\,:\, \mu = 23 \quad vs \quad H_1\,:\, \mu > 23,\]

pois o valor 23 de IMC é considerado um peso mais saudável. Por outras palavras, a questão colocada é:

Haverá alguma possibilidade da população ser considerada obesa ou pré-obesa, em termos médios?

afastamento significativo 

Como rejeitar a hipótese \(H_0\) (\(\mu=23\)) em favor de \(H_1\) (\(\mu > 23\)) usando a média da amostra indicada no enunciado? Por outras palavras, como usar uma amostra para decidir sobre uma população?

Na seguinte figura, a média amostral indica que o parâmetro da população, \(\mu\), não é igual a 23. Fará sentido rejeitar-se a hipótese H0? O que falta?

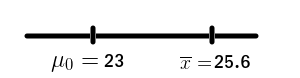
O segmento de reta acima não contempla a variabilidade. Como pensar num contexto de variabilidade de observações?

No exemplo, assume-se o IMC é bem modelado por uma distribuição normal com variância conhecida, \(\sigma^2=4\). Temos

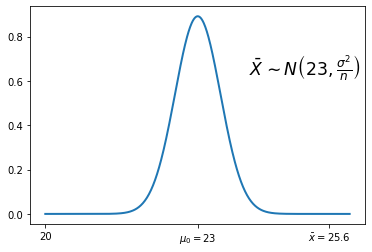
Na figura já se pode ver o afastamento significativo da média populacional, \(\mu_0=23\), à média amostral \(\bar x=25.6\): a probabilidade entre estes dois valores é grande indicando que há muita variabilidade de observações possíveis entre eles.

Se há muita variabilidade entre estes valores poderá o valor 23 representar uma amostra com centro em 25.6? Para que lado tende a decisão?

estatística de teste 

A técnica usual não é trabalhar com a distribuição de \(\bar X\) mas com uma versão centrada e reduzida, isto é, padronizada.

Procedendo a uma «mudança de variável» obtemos a distribuição de amostragem distribuição normal padrão Z:

\[Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \; | \; H_0 \; \sim N(0,\;1)\]

Interpretação: a estatística Z «mede» o afastamento de \(\bar X\) a \(\mu_0\) indicando se a amostra está próxima de H0. Esta contempla a variabilidade (incerteza) no denominador \(\sigma/\sqrt{n}\) e distribuição \(N(0,\;1)\).

teste pelo método do p-value

O método do p-value está implementado no software e em calculadoras gráficas e realiza-se do seguinte modo. Na estatística de teste:

\[Z = \frac{\bar X - \mu}{\sigma/\sqrt{n}} \; | \; H_0 \; \sim N(0,\;1)\]

\(\mu=\mu_0=23\) é valor indicado em H0 e assim, no gráfico de densidade, a origem dos eixos (0,0) ocorre quando não há afastamento entre \(\bar X\) e \(\mu\):

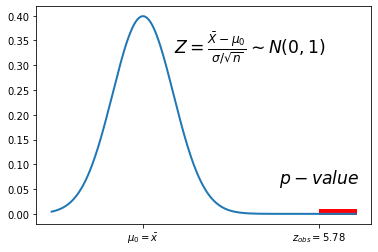
O valor-p, ou p-value, neste teste unilateral à direita, corresponde à probabilidade a vermelho, na imagem:

\[p-value \, = \, P(Z > z_{obs} \;|\; H0) \,= \,P( Z > 5.78) \approx 0.0\]

em que \(z_{obs} = \frac{5.6 - 23}{2/\sqrt{20}} = 5.78\).

O p-value quase nulo indica que \(\bar x= 25.6\) está significativamente longe de \(\mu_0=23\). Quando mais a média de uma dada amostra se afasta de \(\mu_0=23\) menor será o p-value e mais razão se tem para se rejeitar H0.

A regra de decisão é baseada no limiar dado por \(alpha\):

Se \(p-value < \alpha\) então rejeita-se \(H_0\).

A conclusão segue:

rejeita-se H0 em favor de H1, isto é, a média populacional, \(\mu\), é significativamente superior a 23 aos níveis usuais de significância (5%, 10% ou 1%).

A interpreção, no contexto do enunciado, é que

o IMC médio é significativamente superior a 23 sendo esta decisão tomada aos níveis usuais de significância (5%, 10% ou 1%) e com base na amostra apresentada.

Resumo

Consideram-se as hipóteses H0 e H1 sobre o valor médio populacional do IMC:

\(H_0:\, \mu = 23\; vs\; H_1:\, \mu > 23\).

Assim, a questão

como é que uma amostra aleatória pode levar à rejeição de \(H_0\) ?

é vista como

será que a média amostral se afasta estatisticamente muito de \(\mu=23\) conduzindo à rejeição de \(H_0\)?

Por outras palavras, considerando o exemplo \(H_0\,:\,\mu=23\),

se a diferença \(\bar x - 23\) é zero ou estão separadas por uma «pequena probabilidade», então não temos razões para rejeitar H0;
se \(\bar x - 23\) se afasta bastante de zero, isto é, observa-se grande probabilidade no seu distânciamento então temos uma razão para rejeitar H0.

calculadora gráfica e método do |pvalue|

As calculadoras gráficas, e softwares, costumam ter implementados o método do p-value.

Os menus das calculadoras para efetuar um TH costumam estar no menu «estatística».
Deve procurar-se por «Z Interval» ou «Intervalo Z» (para o exemplo apresentando nesta página).
Existe o modo «data» ou «dados»: estes devem ser introduzidos como em dados não agrupados ou dados agrupados.
Existe o modo «stats» ou «estatísticas» (também chamado de modo «variable») para quando um enunciado fornece a média amostral e o desvio padrão populacional.

Exemplo:

texas TI Nspire CX: MENU Estatística (6) => Testes de Hipóteses => Teste Z

teste pelo método da região crítica 

Toma-se o enunciado de exemplo e contexto mencionados nas secções anteriores.

No método da região crítica fixa-se, em primeiro lugar, o nível de significância (recorda-se que é a probabilidade de se cometer um erro de tipo I). Neste exemplo, consideramos que esse nível é \(\alpha=5\%\) e este valor é marcado no gráfico da densidade:

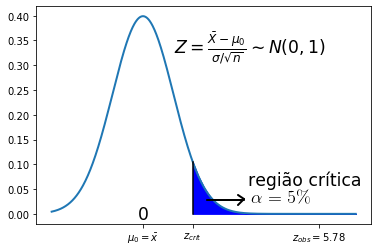
A região crítica, ou região de rejeição de H0, é marcada para a direita, a azul, como indica a hipótese \(H_1\,:\, \mu > 23\) e tem probabilidade \(\alpha=5\%\). O valor crítico, \(z_{critico}\), marca o ponto em que se considera que \(\bar x\) se afasta significativamente de \(\mu=23\).

O valor \(z_{critico}\) é obtido por

\[z_{critico} = INV.Normal(0.95,\; \mu=0,\; \sigma=1)\]

isto é, z é um quantil de ordem 95%.

Conclusão:

Como \(z_{obs}=5.78\) pertence à região crítica então está significativamente afastado de \(\mu=23\). Temos assim uma razão para rejeitar H0 em favor de H1:

o IMC médio é significativamente superior a 23 considerando o nível de significância \(\alpha=5\%\) e com base na amostra apresentada.

teste pelo método do intervalo de confiança 

O método do Intervalo de Confiança é aplicado quando se dispõe de um IC e apenas se usa para testes bilaterais:

\[H_0\,:\, \mu = 23 \quad vs \quad H_1\,:\, \mu \neq 23\]

Conforme apresentando o cálculo do IC é dado por

\[IC_{1-\alpha}(\mu) = \left[ \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right]\]

e substituindo \(\alpha=5\%\), \(\bar x=25.6\), \(\sigma=2\) e n=20 então

\[IC_{95\%}(\mu) = [23.8\,;27.3].\]

Regra:

Se \(\mu_0=23\) está no IC então não se rejeita H0.

Conclusão:

Como \(\mu_0=23\) não pertence ao IC obtido para \(1-\alpha=95\%\) de confiança então rejeita-se H0, o IMC médio é significativamente superior a 23 considerando o nível de significância \(\alpha=5\%\) e com base na amostra apresentada.

pressupostos 

Considerámos, em todo este capítulo, os seguintes pressupostos vindos do enunciado:

uma única população normal com variância conhecida (dada no problema em investigação)

\[X \sim N(\mu, \sigma^2 \text{ conhecida})\]

entendendo-se por «\(\sigma^2\) conhecida» que o problema em investigação do problema em causa fornece a variância populacional.

No caso do enunciado, é indicado que \(\sigma^2=4^2=16\). A desconhecida média populacional, \(\mu\), pode ser confrontada pelos três tipos de hipóteses alternativas (mencionado acima).

etapas gerais do método do p-value

Definir as hipóteses H0 e H1 para o parâmetro de interesse.
Escolher uma estatística de teste T admitindo que H0 é verdadeira.

Lista das estatísticas de teste neste wiki (a letra T indica «Teste» e não apenas distribuição t de Student).

Calcular \(t_{obs}\) que é o valor observado de T para a amostra observada admitindo que H0 é verdadeira.
Determinar o p-value podendo este ser determinado para um teste bilateral ou unilateral.
Decidir com base na regra:

se o p-value\(\le \alpha\) então devemos rejeitar H0 em favor de H1.

se o p-value\(> \alpha\) então não devemos rejeitar H0.

Concluir no contexto do problema.

etapas gerais do método da região crítica 

Região Crítica (RC) ou, também, Região de Rejeição de H0.

Definir as hipóteses H0 e H1 para o parâmetro de interesse.
Escolher uma estatística de teste T admitindo que H0 é verdadeira.

Lista das estatísticas de teste neste wiki (a letra T indica «Teste» e não apenas distribuição t de Student).

Identificar a região crítica (RC) que pode ser unilateral ou bilateral.
Calcular \(t_{obs}\) que é o valor observado de T para a amostra observada admitindo que H0 é verdadeira.
Decidir com base na regra:

se o valor \(t_{obs}\) pertencer à RC então devemos rejeitar H0 em favor de H1.

se o valor \(t_{obs}\) não pertencer à RC então devemos não rejeitar H0.

Concluir no contexto do problema.

etapas gerais do TH com base no IC 

Pressuposto:

o teste a realizar é bilateral (e só esse tipo de teste)

Definir as hipóteses H0 e H1 para o parâmetro de interesse.
Usar ou determinar um IC com grau de confinaça \(1 - \alpha\)
Decidir com base na regra:
- se o valor estipulado em H0 está no IC então não se rejeita \(H_0\);
- se o valor estipulado em H0 não está no IC então não se rejeita \(H_0\);
Concluir no contexto do problema.