intervalo de confiança

Intervalo de Confiança (IC) para a média populacional com estes pressupostos:

• $X \sim N(\mu,\; \sigma^2)$: os dados são bem modelados por uma distribuição normal,

• $\sigma^2$ é conhecida: a variância populacional é fornecida no enunciado ou contexto.

Nessas condições, o IC para a média populacional é dado por:

$$IC_{1-\alpha}(\mu) = \left] \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right[$$

sendo $z_{1-\alpha/2}$ um quantil da distribuição normal padrão.

procedimento

O procedimento, tendo em conta os pressupostos

• $X \sim N(\mu,\; \sigma^2)$: os dados são bem modelados por uma distribuição normal;

• $\sigma^2$ é conhecida: a variância populacional é fornecida no enunciado.

e conhecidas as medidas amostrais, é dado por

$$IC_{1-\alpha}(\mu) = \left[ \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right]$$

em que, com base na distribuição normal padrão Z,

$$z_{1-\alpha/2} = \text{INV.Normal}(1-\alpha/2,\; 0,\; 1)$$

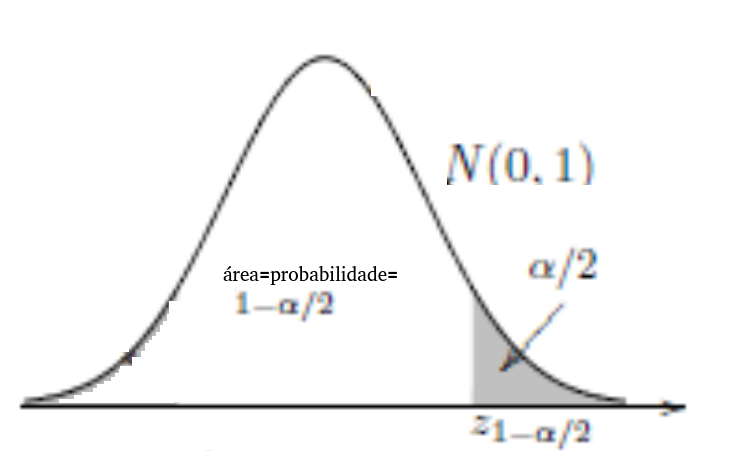
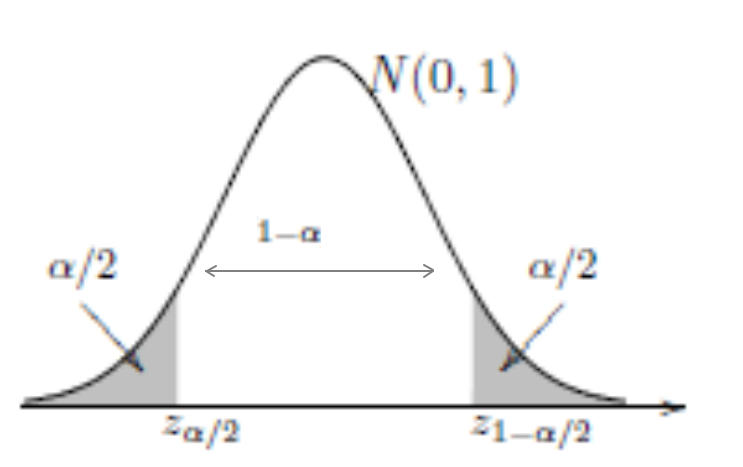
É mostrado, na 2ª figura, que o grau de confiança, $1 - \alpha$, é colocado no centro de N(0,1).

exemplo

Com base no enunciado, o IC com grau de confiança a 95% é dado por:

$$\begin{split}\begin{eqnarray*} IC_{95\%}(\mu) & = & \left] \bar x - z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}},\; \bar x + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right[ \\ & = & \left] 25.585 - z_{1-\alpha/2} \frac{4.0}{\sqrt{20}},\; 25.585 + z_{1-\alpha/2} \frac{4.0}{\sqrt{20}} \right[ \\ \end{eqnarray*}\end{split}$$

Com $1-\alpha=0.95$ então $1-\alpha/2=0.975$. Temos, com base na distribuição normal padrão Z,

$$z_{0.975} = \text{INV.Normal}(0.975,\; 0,\; 1) = 1.96$$

Por fim,

$$\begin{split}\begin{eqnarray*} IC_{95\%}(\mu) & = & \left] 25.585 - z_{1-\alpha/2} \frac{4.0}{\sqrt{20}},\; 25.585 + z_{1-\alpha/2} \frac{4.0}{\sqrt{20}} \right[ \\ & = & \left] 25.585 - 1.96 \times \frac{4.0}{\sqrt{20}},\; 25.585 + 1.96 \times \frac{4.0}{\sqrt{20}} \right[ \\ & = & ]23.8319;27.3381[ \end{eqnarray*}\end{split}$$

propriedades

• o ponto central do IC é $\bar x$, que é a estimação pontual;

• o intervalo pode ser aberto ou fechado e o seus limites não devem ser vistos de forma categórica (i.e., determinística).

• a amplitude do IC é dada por $2 \times z_{1-\alpha/2} \times \frac{\sigma}{\sqrt{n}}$. Porquê?

No exemplo,

• a estimativa $\mu=\bar x = 25.585$ é o centro do intervalo;

• a amplitude do IC é $2 \times 1.96 \times (4.0)/(\sqrt(20)) = 3.5062$.

amplitude do intervalo

• A amplitude do IC é dada por

$$2 \times z_{1-\alpha/2} \times \frac{\sigma}{\sqrt{n}}`$$

• Quanto maior o grau de confiança maior a largura do intervalo. Porquê?

• Quanto maior a amostra, menor a largura do intervalo.

interpretação do intervalo

Um IC para a média populacional pode ser visto como:

• fornecendo a precisão da estimação pontual para $\mu$ [ver 1.]

  • no exemplo dado, $\hat\mu\pm\epsilon = 25.585\pm1.7531$, ou seja, com estimativa $\hat\mu=\bar x = 25.585$ com precisão 1.7531 (a que correponde a amplitude do IC de 3.5062),

ou ainda como,

• um intervalo de valores possíveis para $\mu$ (ver teste pelo método do intervalo de confiança)

  • qualquer valor de $]23.8319;27.3381[$ é uma estimativa para $\mu$.

interpretação da confiança

Tomando como exemplo um grau de confiança é 95% então:

• 95% das amostras conduzem a ICs que vão conter o parâmetro $\mu$ correto que modela a população de onde as amostras são recolhidas.

Dito de maneira probabilística,

• com 0.95 de probabilidade, uma amostra aleatória vai gerar um IC que contém $\mu$, isto é, o parâmetro que modela a distribuição da média amostral aleatória. Veja a construção.

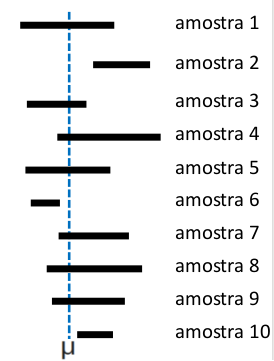
Não se pode interpretar, no entanto, que $\mu \in ]23.8319;27.3381[$ com 95% de probabilidade, pois

• $\mu$ é um número real, e não uma v.a.; assim, não faz sentido calcular uma probabilidade. Seria como calcular «Prob(5 estar em [1; 10])», i.e., ou está ou não está.

construção

Esta secção explica como obter o IC para uma v.a. normal com variância populacional, $\sigma^2$, conhecida (fornecida num enunciado).

Uma população é bem modelada por $X \sim N(\mu,\; \sigma^2)$ e, por distribuição normal (amostragem), então $\bar X \sim N(\mu,\; \frac{\sigma^2}{n})$ ou ainda

$$\frac{\bar X - \mu}{\sigma/\sqrt{n}} \sim N(0,\;1)$$

que diz que o afastamento da média amostral, $\bar X$, à média populacional, $\mu$, é modelado por uma distribuição normal (face às condições dadas). Então, indicamos que esse afastamento não deve ultrapassar certos limites:

$$P( -z \le \frac{\bar X - \mu}{\sigma/\sqrt{n}} \le z ) = 1 - \alpha$$

Transformando a expressão acima,

$$P( \bar X - z \frac{\sigma}{n} \le \mu \le \bar X + z \frac{\sigma}{n} ) = 1 - \alpha$$

Nesta expressão:

• $\mu$ é um número real!

• $\bar X$ é uma média amostral aleatória (logo é uma v.a.)

• os limites, esquerdo e direito, dependem de uma amostra.

A mesma expressão pode-se reescrever assim,

$$P( \text{amostra aleatória gerar um intervalo contendo } \mu ) = 1 - \alpha$$

R Project

Neste capítulo aborda-se apenas o «Z Interval» pois a população é normal com variância conhecida. No R, este intervalo não existe de origem e então é necessário instalar uma biblioteca.

instalação

Deve executar-se a seguinte instrução apenas uma vez:

install.packages("BSDA")

comandos

Com base no enunciado, o IC com grau de confiança a 95% é dado por

library(BSDA)
dados = c(31.2, 22.5, 26.4, 24.2, 26.0, 24.2, 26.5,
          27.8, 26.4, 24.2, 21.6, 28.8, 23.9, 29.8,
          25.0, 25.4, 24.0, 28.7, 21.9, 23.2)
z.test(dados, sigma.x=4.0, conf.level = 0.95)

sendo o resultado:

One-sample z-Test

data: dados

z = 28.605, p-value < 2.2e-16

alternative hypothesis: true mean is not equal to 0

95 percent confidence interval:

23.83195 27.33805

sample estimates:

mean of x

25.585

• Referência: http://genomicsclass.github.io/book/pages/confidence_intervals.html

calculadora gráfica

• Os menus das calculadoras para determinar IC costumam estar no menu «estatística».

• Em geral, deve procurar-se por «Z Interval» ou «Intervalo Z».

• Existe o modo «dados»: devem ser introduzidos como em dados não agrupados ou dados agrupados.

• Existe o modo «stats» (ou ainda modo «variable»).

Exemplo:

• texas TI Nspire CX: MENU Estatística (6) => Intervalo de Confiança (6) => Intervalo Z (1)