guia para a conversão de p-values

contexto

O seguinte guia aplica-se quando:

• foi efetuado um teste para uma população

• do teste feito, resultou um p-value bilateral

O mecanismo de conversão é similar para o caso dos parâmetros populacionais da média (\(\mu\)), desvio (\(\sigma\)), variância (\(\sigma^2\)) ou proporção (\(p\)).

exemplo

Sem perda de generalidade vamos assumir um exemplo de um teste bilateral para a média (\(\mu\)):

\[H_0: \mu = 10 \quad vs \quad H_1: \mu \neq 10\]

e para o qual o p-value bilateral foi 6%.

conversão do p-value para teste à direita

Pretende-se efetuar o teste unilateral à direita, para o exemplo dado,

\[H_0: \mu = 10 \quad vs \quad H_1: \mu > 10\]

Importante

Caso 1 A média da amostra \(\bar x\) é maior que 10.

Vamos considerar que a média amostral foi \(\bar x=12\).

Como a amostra tem média \(\bar x=12\) então dizemos que a amostra aponta no mesmo sentido de \(H_1\) pois

A média amostral \(\bar x=12\)	A hipótese alternativa \(H_1\) diz que
é tal que \(\bar x > 10\)	\(\mu > 10\)

pois ambas, amostra e H1, usam \(>\).

Conclusão: A expressão a aplicar é:

\[\text{p-value unilateral} = \frac{\text{p-value bilateral}}{2}\]

A resposta, neste exemplo, seria que p-value unilateral à direita é 3%.

origina

Importante

Caso 2 A média da amostra \(\bar x\) é menor que 10.

Vamos considerar que a média amostral foi \(\bar x=8\).

Como a amostra tem média \(\bar x=8\) então dizemos que a amostra aponta em sentido contrário a \(H_1\) pois

média amostral \(\bar x=8\)	hipótese alternativa \(H_1\)
\(\bar x < 10\)	\(\mu > 10\)

Conclusão: A expressão a aplicar é

\[\text{p-value unilateral} = 1 - \frac{\text{p-value bilateral}}{2}\]

A resposta, neste exemplo, seria que p-value unilateral à esquerda é \(1-6\%/2=97\%\).

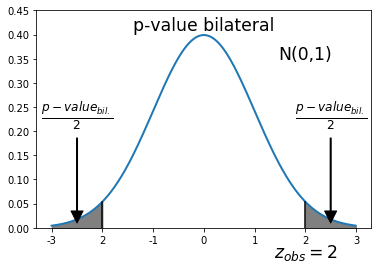
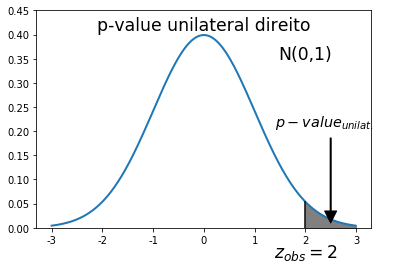
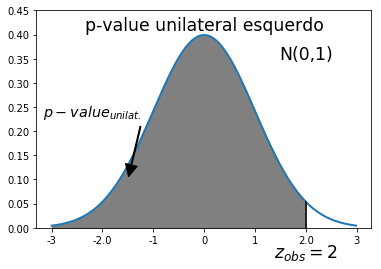
As imagens mostram o p-value bilateral e o p-value unilateral.

origina

conversão do p-value para teste à esquerda

Análogo ao texto acima.