quantil populacional

Um quantil $x_p$ é um valor de uma v.a. X que envolve uma probabilidade p tal que

$$P(X \le x_p) = p$$

No exemplo da imagem, o quantil $x_{0.25}$ indica um valor no eixo do XX atrás do qual a probabilidade é 25%:

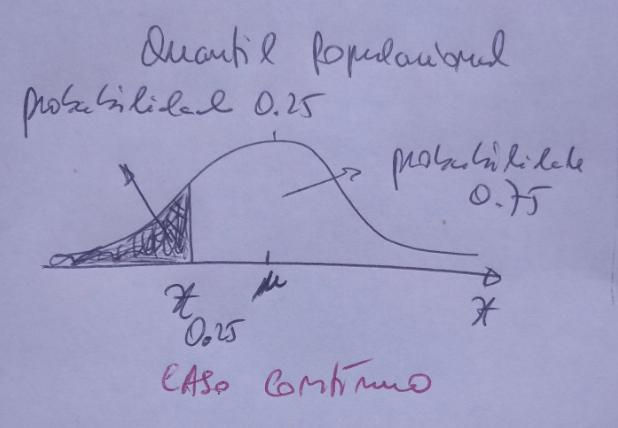
É necessário usar «quantil» e não apenas o «valor» pois quantil envolve também a probabilidade igual ou inferior ao valor.

descrição

Dada uma probabilidade p, um quantil populacional é um valor q que verifica:

$$P(X \le q) = p$$

em que X é uma v.a. com função distribuição $F(x)=P(X \le x)$ (ou seja, um modelo matemático para as probabilidasdes da v.a. X).

Se a v.a. for discreta pode existir mais que um valor possível para q. Em geral, no caso contínuo, só existe um único valor q (uma das exceções é a distribuição uniforme não apresentada nesta documentação).

caso discreto

No caso discreto pode existir mais que um quantil de ordem p. A definição é similar à definição de quantil amostral:

• Um quantil de ordem $p$ (com $0 \le p \le 1$) é um valor, $x_p$, que divide a reta real em duas partes, tal que

$$P(X \le x_p) \ge p \quad \text{ e, também, }\quad P(X \ge x_p) \ge (1-p)$$

Por exemplo, um quantil $x_{0.25}$ deve verificar

$$P(X \le x_{0.25}) \ge 0.25 \text{ e } P(X \ge x_{0.25}) \ge 0.75$$

ou seja,

• à esquerda de $x_{0.25}$ ocorre uma probabilidade não inferior a $0.25$

• e, também deve ser verificado, que

• à direita de $x_{0.25}$ ocorre uma probabilidade não inferior a $0.75$.

caso contínuo

Um quantil de ordem $p$ (com $0 \le p \le 1$) é um valor, $x_p$, que divide a reta real em duas partes, tal que

$$P(X \le x_p) = p$$

que também pode ser escrito, com a função de distribuição, por $F(x_p) = p$. A imagem ilustra o quantil, a probabilidade p e a probabilidade 1-p:

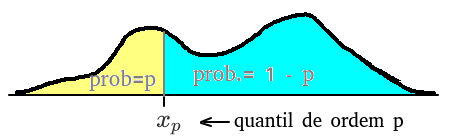
Notas:

1. Se $F(x_{0.25}) = 0.25$ então para conhecer $x_{0.25}$ temos que conhecer a função inversa de F(), por tabelas ou usando calculadora gráfica.

2. No caso de x ser um valor que obedece a $P(X \ge x) = p$ então x não se designa por quantil. Usando a relação

$$P(X \ge x) = p \Leftrightarrow P(X \le x) = 1-p$$

vê-se que x é um quantil de ordem 1-p.

quartis, decis, percentis populacionais

Usando a notação $x_p$, definem-se os termos:

• quartis: $Q_1=x_{0.25}$, $Q_2=x_{0.50}$, $Q_3=x_{0.75}$;

• decis: $D_1=x_{0.1}$, $D_2=x_{0.2}$, etc, $D_9=x_{0.9}$;

• percentis: $P_1=x_{0.01}$, $D_2=x_{0.02}$, etc, $P_{99}=x_{0.99}$.

seja em termos de v.a. discreta, como v.a. contínua.