variável aleatória (v.a.)

Ilustra-se o conceito de variável aleatória através de exemplos:

  • X = «número de dias em que choveu na cidade de Aveiro ao longo de um ano»;

  • X = «comprimento de um robalo (Dicentrarchus labrax) pescado na costa portuguesa»;

  • X = 0 ou 1 (0 se é macho; 1 se é fêmea);

  • X = 0 ou 1 (0 se não chove num dia; 1 se chove num dia).

Uma variável aleatória é sempre descrita por um número obtido de uma escala contínua ou discreta.

variável aleatória e concretização

Uma variável aleatória, designada habitualmente pela letra maiúscula X, designa um número real (na escala discreta ou contínua) que mede algo de um indivíduo, objeto ou elemento:

  • se o indivíduo é um robalo então várias v.a. podem ser medidas:

    • X = «peso de um robalo»

    • X = «comprimento de um robalo»

  • se o elemento é um dia, do ano civil, então várias v.a. podem ser medidas:

    • X = 0 «se não chove num dia»; 1 «se chove num dia»;

    • X = «precipitação (mm) em duas horas»

    • X = «duração total de periodos de sol em um dia».

  • se o objeto é uma peça de fruta, então várias v.a. podem ser medidas:

    • X = 0 «se a cor não é amarela»; 1 «se a cor é amarela»;

    • X = «peso de uma peça de fruta»;

Consideremos agora concretizações efetivas das v.a., usando a letra minúscula x:

  • do robalo capturado, e devolvido ao mar, observou-se:

    • x = 1.5Kg de peso;

    • x = 55cm de comprimento ;

  • no dia 2/março/2020, foi observado que

    • x = 1 (isto é, choveu);

    • x = 2mm (em duas horas);

    • x = 6hr.

  • considerando a laranja que tenho na mão:

    • x = 0 (a cor não é amarela);

    • x = 150gr.

definição formal

Apresenta-se uma definição um pouco mais formal.

Seja \Omega um conjunto de elementos designados por \omega. O conjunto \Omega também se designa de universo ou espaço dos possíveis.

Exemplo:

  • O conjunto \Omega é a coleção de cartas: «Ás», «Rei», «Dama», «Valete», «10», «9», etc, «2» para cada um dos naipes. Este conjunto \Omega tem 52 elementos em que um deles é \omega= «Ás de paus». (Ver jogo da Sueca.)

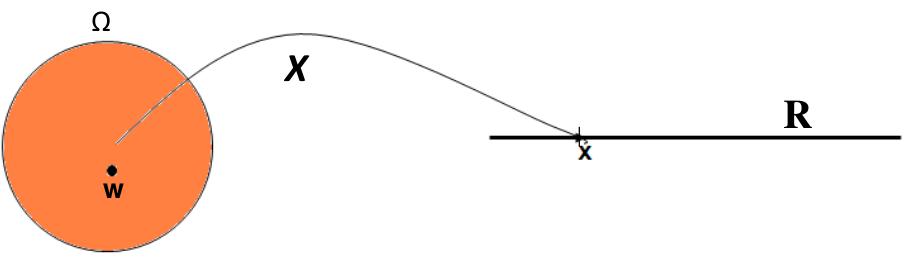
Uma variável aleatória, X, é uma função com domínio \Omega e com contradomínio nos números reais R. Assim, X associa um número real x a um elemento \omega.

Exemplo:

  • X = valor da carta retirada à sorte de uma baralho completo de 52 cartas.

_images/va-definicao.png

  • Veja outra imagem mais detalhada aqui.

Continuação do exemplo:

  • No citado jogo da Sueca costuma-se fazer esta atribuição: os «Áses» valem 11 pontos, os «Setes» valem 10 pontos, os «Reis» valem 4 pontos, os «Damas» três e os «Valetes» apenas dois pontos. As restantes cartas (palha) valem 0 pontos. Os diferentes valores reais são 11, 10, 4, 3, 2 e 0.

    • X toma valores em \{0,2,3,4,10,11\}, isto é, o contra domínio de X é \{0,2,3,4,10,11\}.

A probabilidade de ocorrer um intervalo real é igual à probabilidade dos acontecimentos que lhe deram origem:

  • no exemplo: se ocorre o intervalo [4,\,11] então pode ter saído qualquer «Ás», qualquer «Sete» ou, ainda, qualquer «Rei».

representações de uma v.a.

Para representar uma v.a. usam-se as letra maiúsculas X ou Y. Também, mas menos frequentemente, usam-se as letras maiúsculas T, V, W, Z ou outras.

Uma amostra aleatória é uma coleção de n variáveis aleatórias designadas por: X_1,\, X_2,\, X_3,\, \ldots,\, X_n.

Dica

Nos problemas estudados deve sempre começar por se identificar as variáveis aleatórias em estudo, nesta forma:

X = valor de uma carta retirada à sorte de uma baralho completo de 52 cartas

Uma experiência resulta num elemento observado de uma conjunto maior. Uma v.a. resulta em um número real associado a esse elemento observado.

As concretizações das v.a. denotam-se pelas respectivas letras minúsculas (x,y,t,v,w,z) sendo que estas representam números reais concretos.

Dica

x = valor do ás de espadas = 11 pontos.

exemplos

Dois exemplos conhecidos da comunidade de Bioestatística em Aveiro são

A definição de uma v.a. é feita de forma abstrata: «de um canal» ou «num ano», sem especificar qual o objeto concreto. Os exemplos, não indicam qual o canal da ria ou qual o ano.

Se concretizarmos o canal da ria ou o ano então teremos uma concretização, e utiliza-se letra minúscula x:

  • x=35g/kg (salinidade em g/kg);

  • x=20 golfinhos capturados em 2011.

notação X=x

Dois exemplos habituais de notação são:

  • X=x

  • a \le X \le b

A notação X=x representa a afirmação:

quais os acontecimentos elementares que ocorrem quando a variável aleatória X toma o valor real x

No exemplo das cartas,

  • X=11 representa o evento de que um qualquer «Ás» tenha ocorrido: {Ás de paus, Ás de espadas, Ás de copas, Ás de ouros}.

As palavras evento, ou acontecimento, têm o significado comum e representam um ou mais elementos \omega de um universo \Omega.

Ainda no mesmo exemplo,

  • se 4 \le X \le 11 significa que pode ter saído qualquer «Ás», qualquer «Sete», ou ainda, qualquer «Rei» (um total de 12 cartas possíveis).

referências