distribuição contínua

Uma distribuição é uma função que permite atribuir probabilidades.

No caso de uma v.a. contínua é atribuída uma probabilidade a qualquer intervalo de valores reais da v.a.:

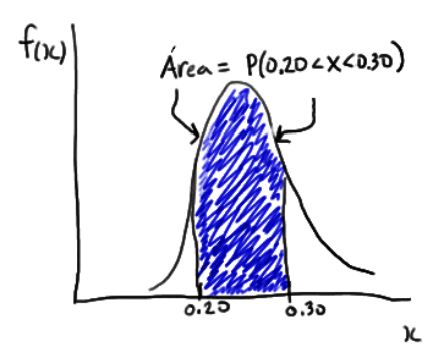
Uma distribuição, no caso contínuo, tem duas formas equivalentes:

• função densidade de probabilidade: \(f(x)\) que a cada x atribui uma densidade, ou um «peso», mas não uma probabilidade;

• função de distribuição: \(F(x)=P(X \le x)\).

Dica

Valores pontuais têm, neste modelo matemático contínuo, a probabilidade zero. Ou seja: \(P(X=a)=0\) para qualquer valor a.

propriedaes

1. No caso de v.a. contínua, o modelo matemático é feito com:

\[P(X=a) = 0 \text{ para qualquer constante real $a$ }\]

Por exemplo, se X for a altura de uma pessoa? Qual a probabilidade de uma pessoa medir 1.60m? Como são as áreas que dão as probabilidades então,

\[P(1.60-0.005 \le X \le 1.60+0.005) \text{ determina a probabilidade de uma pessoa ter "1.60m" }\]

ou ainda \(P(1.595 \le X \le 1.605)\).

2. Uma vez que as probabilidades pontuais são nulas temos (com a uma constante real):

\[P(X < a) = P(X \le a)\]

\[P(X > a) = P(X \ge a)\]

3. O mesmo se aplica a intervalos \([a,b]\):

\[P(a < X < b) = P(a \le X \le b) =\]

\[= P(a < X \le b) = P(a \le X < b)\]

4. Quando as calculadoras, ou software, não determinam probabilidades em intervalos, considere ainda:

\[P(a \le X \le b) = P(X \le b) - P(X \le a)\]

sendo indiferente o uso de \(\le\) ou \(<\).