Ex 2.27 (*)

Seja X a v.a. que representa o número de filhos fêmea que um animal adulto tem em 3 anos. Esta variável tem a seguinte distribuição genérica:

x	0	1	2	3	4
P(X=x)	0.03	0.19	0.44	0.30	0.04

(a) Calcule o valor esperado (ou média populacional) do número de crias fêmea.

☞ sugestões

• média populacional

☞ proposta de resolução

$$\begin{split}\begin{eqnarray*} E(X) & = & \sum_{i=1}^5 x_i P(X=x_i) \\ & = & 0 \times 0.03 + 1 \times 0.19 + 2 \times 0.44 + 3 \times 0.30 + 4 \times 0.04 \\ & = & 2.13 \end{eqnarray*}\end{split}$$

(b) Calcule o desvio padrão populacional do número de crias fêmea.

☞ sugestões

• variância populacional

☞ proposta de resolução

Seja $\mu=E[X] = 2.13$ conforme a alínea anterior.

$$\begin{split}\begin{eqnarray*} \sigma^2 & = & Var(X) \\ & = & \sum_{i=1}^5 (x_i - \mu)^2\, P(X=x_i) \\ & = & (0 - 2.13)^2 \times 0.03 + (1 - 2.13)^2 \times 0.19 + \\ & & (2 - 2.13)^2 \times 0.44 + (3 - 2.13)^2 \times 0.30 + (4 - 2.13)^2 \times 0.04 \\ & = 0.7531 \end{eqnarray*}\end{split}$$

O desvio padrão populacional segue usando a raiz quadrada da variância populacional:

$$\sigma = \sqrt{ V(X) } = \sqrt{ 0.7531 } = 0.8678133$$

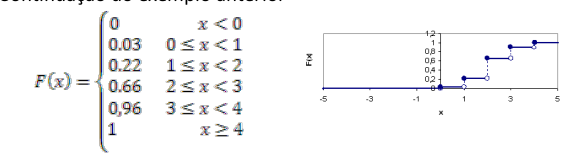
(c) Determine a função de distribuição.

☞ sugestões

Esta função é análoga à função de distribuição empírica. Realize o ex. 1.26 (*) primeiro.

☞ proposta de resolução

A função de distribuição (fd), F, de uma variável discreta é uma função em forma de escada não decrescente, começando, em geral, no patamar zero e atingindo o patamar 1.