pressupostos e sua validação

modelo

O modelo linear simples rege-se por

$$\begin{align}\begin{aligned}Y|x = \beta_0 + \beta_1 x + \epsilon, \quad \beta_1 \neq 0,\\\epsilon \sim N(0, \; \sigma^2)\end{aligned}\end{align}$$

onde é patente o pressuposto de que o erro é uma v.a. com distribuição normal centrada em 0 e variância $\sigma^2$.

A variância $\sigma^2$ não depende da posição x ou y.

erro e resíduos

A obtenção de concretizações do erro aleatório, $\epsilon$, processa-se obtendo os resíduos, $e_i$, para uma dada amostra.

Considerando uma amostra de n observações emparelhadas $(x_i,y_i)$:

$$(x_1,y_1),\ldots,(x_n,y_n)$$

temos

$$y_i = \beta_0 + \beta_1 x_i + e_i, \quad i=1, \ldots, n$$

como ilustra a imagem:

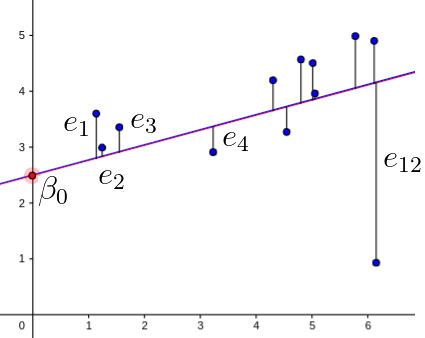
onde

• os valores $x_i$ são provenientes de uma variável independente também denominada regressor ou variável explicativa;

• os valores $y_i$ são dependentes e são a resposta a $x_i$;

• os resíduos $e_i$ são valores independentes obtidos por

$$e_i = y_i - \hat y_i \quad \text{ em que } \hat y_i = \beta_0 + \beta_1 x_i$$

pressupostos da regressão

O erro no modelo de regressão linear simples, $\epsilon$, é uma v.a. que verifica

$$\epsilon \sim N(0, \sigma^2)$$

sendo os resíduos, $e_i$ uma coleção de observações da v.a. $\epsilon$.

Assim, a amostra de resíduos deve:

• verificar a independência face a x ou $\hat y|x$;

• ser bem modelada por uma distribuição normal;

• em que a variância não depende de x ou $\hat y|x$.

procedimento para validação dos pressupostos

1. Gráfico dispersão de resíduos

Realiza-se um gráfico de dispersão entre

• valores preditos $\hat y_i$ (eixo xx)

• resíduos $e_i$ (eixo yy)

1. (a) No gráfico de dispersão deve observar-se que há aleatoriedade e esta que significa independência face a valores preditos $\hat y_i$.

No seguinte gráfico é verificada a independência face a $\hat y_i$ pois há aleatoriedade.

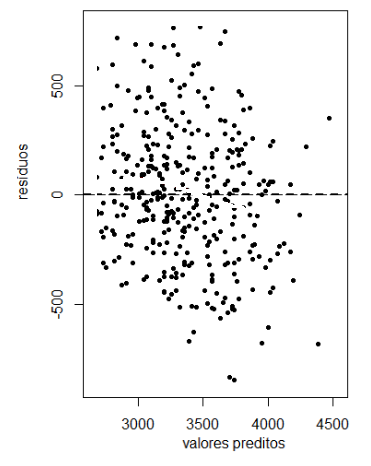
No seguinte gráfico não há aleatoriedade pois os resíduos $e_i$ dependem de x (poderia ser também $\hat y_i$):

1. (b) No gráfico de dispersão deve observar-se que a variabilidade é constante ao longo de x ou de $\hat y_i$. Por outras palavras, a variância do erro não depende de x ou dos valores preditos $\hat y_i$.

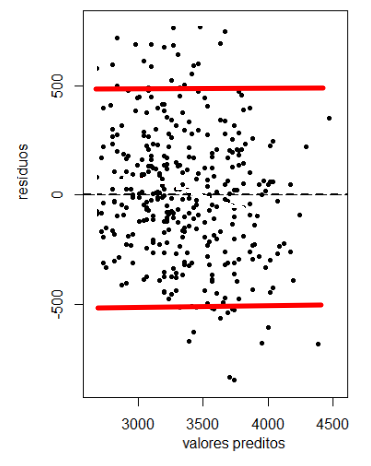
No seguinte gráfico não há constância da variabilidade ao longo de x (poderia ser também $\hat y_i$):

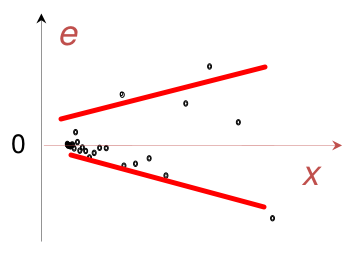
2. Ajustamento à normalidade

Como $\epsilon \sim N(0, \; \sigma^2)$ então é necessário verificar se a coleção resíduos, obtidos pela regressão linear sobre uma amostra $(x_i,y_i)$, é bem modelada por uma distribuição normal. Em ajustamento à normal são apresentadas as técnicas para esse fim e que aqui são reproduzidas e sumariadas:

2. (a) QQ plot normal

Comparam-se os quantis da amostra de resíduos $e_1,\ldots,e_n$ com os quantis de uma distribuição normal obtem um gráfico «QQ plot» como o da seguinte figura:

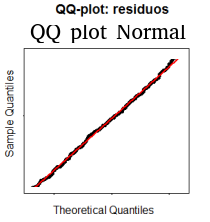
Os pontos devem ser próximos à «reta de quantis» para não se rejeitar a normalidade dos resíduos, confirmando o modelo de que $\epsilon \sim \text{normal}$.

2. (b) Testes de Hipóteses de ajustamento à normal

Se a amostra tem dimensão inferior a 30 pares de observações então deve realizar-se o teste de Shapiro-Wilk.

Caso contrário deve realizar-se o teste Kolmogorov-Smirnoff com correção Lilliefors.

Em ambos os casos obtém-se um p-value que não deve conduzir à rejeição da normalidade (p-value elevado).

Complemento: o sistema R oferece uma tabela como a seguinte:

na qual se podem ver as principais medidas amostrais dos resíduos: nela pode ser apreciada a simetria e amplitude dos valores dos resíduos.

A secção R Project introduz rotinas online com as quais se obtém a reta de regressão linear simples paramétrica e efetua-se a verificação dos pressupostos.