significado da regressão
Será que Y depende de x?
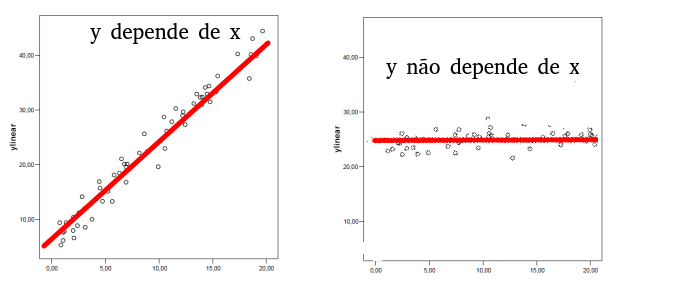
diagrama de dispersão
O diagrama de dispersão deve mostrar evidência da dependência, em média, de y face a x:
teste de hipóteses sobre o parâmetro do declive
Além da informação visual deve ser realizado um teste de hipóteses ao declive \(\beta_1\):
Este teste de hipóteses efetua-se com base na distribuição t de Student, com n-2 graus de liberdade, como pode ser lido na secção inferência da regressão.
Com base no R ou calculadoras é obtido o p-value ao coeficiente de regressão \(\beta_1\) (declive). Um exemplo encontra-se na imagem, em que o p-value se encontra na caixa vermelha:
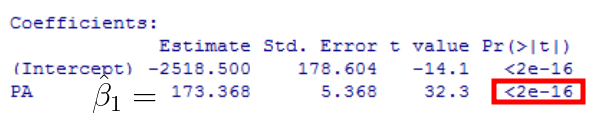
A regra é a usual:
se o p-value do teste ao declive \(\beta_1\) for inferior ao níveis usuais de significância então rejeita-se H0. A interpretação é que o declive é significativamente difernete de zero ou seja a regressão faz sentido: os valores y médios dependem significativamente de x.
caso contrário, p-value superior aos níveis usuais de significância, a regressão não faz sentido e os valores y médios não dependem significativamente de x.
As calculadoras gráficas e o software estatístico realizam os cálculos com base na amostra fornecida por forma à obtenção do p-value para o teste mencionado:
tabela de output do R
A imagem contém um exemplo de tabela de output do software R para a regressão linear simples:

Os campos da tabela «Coefficients» são:
Estimate |
Std. Error |
t value |
p-values |
|
(Intercept) |
\(\hat \beta_0\) |
\(\hat \sigma_0\) |
\(t_{obs,0}\) |
p-value de \(\beta_0\) |
variável x |
\(\hat \beta_1\) |
\(\hat \sigma_1\) |
\(t_{obs,1}\) |
p-value de \(\beta_1\) |
Mais informação em inferência da regressão.