regressão linear simples

É apresentado um método para modelar uma relação causal linear (ver esboço de uma reta afim) entre duas variáveis:

\[y = \beta_0 + \beta_1 x, \quad \beta_1 \neq 0,\]

Os coeficientes são obtidos a partir de uma amostra de observações emparelhadas \((x_i, y_i)\) e do seguinte modelo da regressão linear simples (modelo paramétrico):

\[Y|x = \beta_0 + \beta_1 x + \epsilon, \quad \beta_1 \neq 0,\]

em que

\[\epsilon \sim N(0, \; \sigma^2)\]

exemplo e motivação

São exemplos de aplicação:

• Avaliar o crescimento de uma planta, em função da concentração de zinco.

• Avaliação do efeito da poluição no crescimento dos seres de uma determinada espécie.

• Construir um modelo de previsão do peso fetal à nascença com base no perímetro abdominal da mãe.

A motivação é que uma vez estabelecida uma reta podemos calcular valores preditos y para qualquer x num domínio apropriado:

• dada uma concentração de zinco, pode-se obter o crescimento esperado de uma planta;

• dada uma concentração de poluente, pode-se obter o efeito médio do crescimento de seres expostos à poluição;

• dado um perímetro abdominal, pode-se obter o peso esperado do peso à nascença.

esboço de uma reta afim

Uma reta nem horizontal, nem vertical, designa-se por função afim e escreve-se com a seguinte notação:

\[y = \beta_0 + \beta_1 x\]

em que

• \(\beta_0\) é a ordenada na origem; em algumas calculadoras este é o coeficiente «a»;

• \(\beta_1\) é o declive da reta; em algumas calculadoras este é o coeficiente «b».

Um esboço da reta de regressão requer dois pontos e um domínio no eixo xx. No seguinte exemplo, o domínio é de 0 a 2:

Para esboçar a reta, no domínio indicado, foi necessário calcular e marcar dois pontos:

• ponto (0,0.5): em \(x=0\) obtemos \(y=\beta_0 + \beta_1 \times 0\), isto é, o ponto \((x=0,y=0.5)\) sem quaisquer cálculos;

• ponto (2,2): em \(x=2\) obtemos \(y = 0.5 + 0.75 \times 2=2\), ou seja, o ponto \((x=2,y=2)\).

não há regressão

Diz-se que não há regressão se o declive for nulo pois o valor de y não é determinado pelo valor de x. O exemplo mostra essa possibilidade que, no entanto, carece de teste estatístico ao declive \(\beta_1\) (ver significado da regressão):

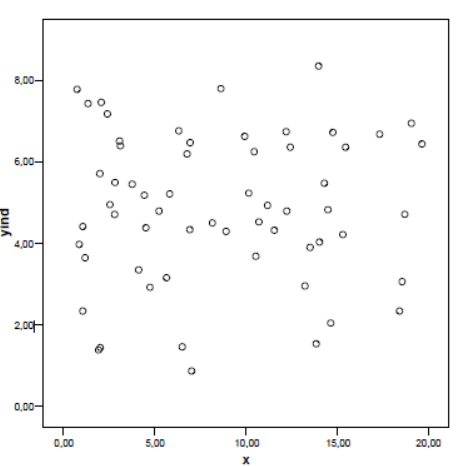
modelo linear de regressão simples

O modelo de regressão linear simples relaciona a variável dependente \(y\) (também designada por «variável explicada» ou «variável resposta») com uma variável independente \(x\) (também designada por «variável explicativa») resultando no seguinte modelo:

\[ \begin{align}\begin{aligned}Y|x = \beta_0 + \beta_1 x + \epsilon\\\epsilon \sim N(0, \; \sigma^2)\end{aligned}\end{align} \]

sendo:

• \(\beta_0\): a ordenada na origem dos eixos;

• \(\beta_1\): o declive;

• erro aleatório \(\epsilon\): modela o erro associado a cada observação Y.

A imagem apresenta uma situação típica de modelaçao por regressão linear simples:

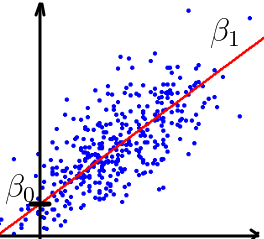
obtenção da reta

A reta de regressão é obtida tendo uma amostra de n observações emparelhadas \((x_i,y_i)\):

\[(x_1,y_1),\ldots,(x_n,y_n)\]

que na imagem acima são representadas pelos pontos a azul. Para se obter a reta de regressão é esboçada a técnica do «método dos mínimos quadrados» de seguida.

método dos mínimos quadrados

Usando um método apresentado nos aspetos teóricos determina-se uma reta estimada que se representa por:

\[\hat y|x = \hat \beta_0 + \hat \beta_1 x\]

em que:

• \(\hat y|x\) designa um valor predito de y para um dado x;

• \(\hat \beta_0\) designa uma estimativa de \(\beta_0\) para os pontos \((x_1,y_1),\ldots,(x_n,y_n)\);

• \(\hat \beta_1\) designa uma estimativa de \(\beta_1\) para os pontos \((x_1,y_1),\ldots,(x_n,y_n)\).

A técnica matemática designa-se por método dos mínimos quadrados e determina a reta que minimiza as áreas quadradadas a amarelo na seguinte imagem:

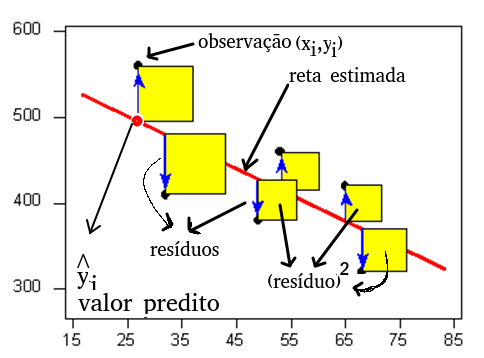
As aplicações ilustram o mecanismo de procura dos mínimos quadrados:

• jogo: posicione a reta

• versão leve

erros e resíduos

Por vezes há necessidade de usar uma terminologia rigorosa:

• erro: é a v.a. que modela o erro associado a cada observação Y, sendo estes centrados em 0 e com variância \(\sigma^2\) e bem modelados por uma distribuição normal;

• resíduo: é um valor real que mede o afastamento da reta à observação. A imagem mostra uma reta (reta a vermelho) preditiva obtida a partir de pares de observações \((x_i,y_i)\) (bolinhas a preto) em que os afastamentos à reta se designam por resíduos (segmentos a azul):

Assim, um resíduo é a diferença entre o valor observado \(y_i\) e o valor predito pela reta.

valor predito

Uma motivação para a obtenção de retas é pode estimar-se o valor da variável dependente (y) para um dado (x):

\[\hat y | x= \hat \beta_0 + \hat \beta_1 x\]

• em que \(\hat y | x\) designa o valor predito pela reta de regressão sabendo x;

  • (valor predito ou valor estimado para y)

• \(\hat \beta_0\): ordenada na origem estimada

  • nas calculadoras costuma ser a letra «a»;

• \(\hat \beta_1\): declive estimado

  • nas calculadoras costuma ser a letra «b».

No exemplo da reta acima, para \(x=1.5\), podemos obter o valor predito:

• \(\hat y =0.5 + 0.75 \times 1.5 \approx 1.625\)