aspetos teóricos

Notação, conceitos e expressões sobre a regressão linear.

método dos mínimos quadrados

Os estimadores de mínimos quadrados dos coeficientes da reta de regressão são dados por

\[\begin{split}\left\{ \begin{array}{l} \hat \beta_1 = \displaystyle \frac{S_{xY}}{S_{xx}} \quad \leftarrow \text{declive}\\ \hat \beta_0 = \bar Y - \hat \beta_1 \bar x \quad \leftarrow \text{ordenada na origem}\\ \end{array} \right.\end{split}\]

sendo

\[\begin{split}\begin{eqnarray*} S_{xx} & = & \sum_{i=1}^n (x_i - \bar x)^2 \\ S_{xY} & = & \sum_{i=1}^n (x_i - \bar x)(Y_i - \bar Y) \\ \end{eqnarray*}\end{split}\]

e a reta de regressão é então

\[y = \hat \beta_0 + \hat \beta_1 x\]

Note-se que o par \((\bar x, \bar Y)\) pertence à reta de regressão estimada e a segunda equação usa esta propriedade para determina \(\beta_0\).

construção dos estimadores

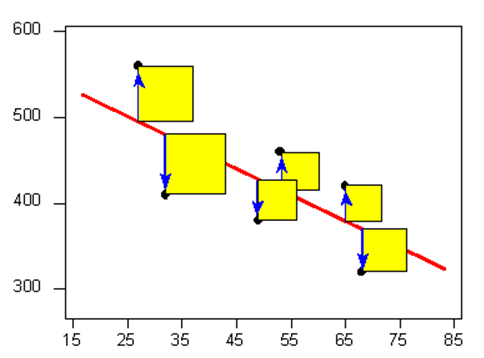
_images/rl-estimacao.png

Por fazer

a fazer a estimação de beta0 beta1 e sigma

Os parâmetros do modelo de regressão linear são estimados através dos mínimos quadrados.

inferência beta0 e beta1

_images/rl-estimacao.png

Os parâmetros do modelo de regressão linear são estimados através dos mínimos quadrados.

Os estimadores de mínimos quadrados dos coeficientes da reta de regressão são dados por

\[\begin{split}\left\{ \begin{array}{l} \beta_0 = \bar Y - \beta_1 \bar x \\ \beta_1 = \frac{S_{xY}}{S_xx} \end{array} \right.\end{split}\]

sendo

\[\begin{split}\begin{eqnarray*} S_{xx} & = & \sum_{i=1}^n (x_i - \bar x)^2 \\ S_{xY} & = & \sum_{i=1}^n (x_i - \bar x)(Y_i - \bar Y) \\ \end{eqnarray*}\end{split}\]

inferência na regressão

Testes e ICs para os coeficientes de regressão Com base em resultados teóricos é possível construir intervalos de confiança e efetuar testes de hipóteses aos parâmetros do modelo de regressão. Esses resultados correspondem ao conhecimento das seguintes distribuições de amostragens:

Os estimadores dos parâmetros e suas propriedades são

\[\begin{array}{lll} \hat \sigma^2 = \displaystyle \frac{SS_E}{n-2} ~~~ &\displaystyle \frac{(n-2)\hat \sigma^2}{\sigma^2}=\displaystyle \frac{SS_E}{\sigma^2}\frown \chi^2_{(n-2)} ~~~ & T_i=\displaystyle \frac{\hat\beta_i-\beta_i}{\hat\sigma_{\beta_i}} \frown t_{n-2} \end{array}\]

podendo assim serem feitos testes como

\[\begin{split}\begin{array}{l} H_0:~\beta_0=0~~vs~~H_1:~\beta_0\neq 0 \quad\leftarrow\text{Teste à ordenada na origem} \\ H_0:~\beta_1=0~~vs~~H_1:~\beta_1\neq 0 \quad\leftarrow\text{Teste ao declive} \\ H_0:~\sigma^2=0~~vs~~H_1:~\sigma^2>0 \quad\leftarrow\text{Teste à var. dos erros} \\ \end{array}\end{split}\]

A tabela de regressão habitual no R contém os testes individuais aos parâmetros $beta_i$:

\[\begin{split}\begin{array}{cccccc} \text{Coeficiente~} & {~\beta} & \text{Erro padrão} & t_{obs} & \pvalue \\ \hline \text{Ord.Origem} & ~\hat \beta_0 & \hat \sigma(\beta_0) & t_{0,obs} & (\cdot)\\ \text{declive} x & ~\hat \beta_1 & \hat \sigma(\beta_1) & t_{1,obs} & (\cdot) \\ \end{array}\end{split}\]

construção do coeficiente \(R^2\)

A variação total \(S_{YY}\) face à média \(\bar Y\) é dada por

\[S_{YY} = \sum_{i=1}^n (Y_i-\bar Y)^2 \quad \text{(variação total)}\]

e pode ser decomposta nas suas componentes de regressão e erro.

\[S_{YY} = SS_R + SS_E\]

em que:

  • a variação devido à reta de regressão, \(\hat y|x=\beta_0 + \beta_1 x\), é

\[SS_R=\sum_{i=1}^n (\hat Y_i-\bar Y)^2\]

(SS quer dizer «sum of squares» e é a notação habitual).

  • a variação devido aos erros, \((Y|x - \hat y|x) \sim N(0,\sigma^2\), é

\[SS_E=\sum_{i=1}^n (Y_i-\hat Y_i)^2\]

coeficiente de determinação

Pode ser calculado com duas interpretações complementares:

  • \(R^2\) como percentagem explicativa da variação de Y face a x (devida à reta de regressão):

\[R^2 = \displaystyle \frac{\text{variação em Y causada pela variação em x}}{\text{variação total}} = \displaystyle \frac{SS_R}{S_{YY}}\]

  • \(R^2\) como (100% - percentagem de variação devida aos erros):

\[R^2 = 1 - \displaystyle \frac{\text{var. dos erros}}{\text{variação total}} = \displaystyle 1-\frac{SS_E}{S_{YY}}\]

inferência sigma^2

Pretende-se:

  • construir intervalos de confiança

  • efetuar testes de hipóteses

ao parâmetro \(\sigma^2\).

Estimação

\[\hat \sigma^2 = \displaystyle \frac{SS_E}{n-2}\]
\[\frac{(n-2)\hat \sigma^2}{\sigma^2} = \displaystyle \frac{SS_E}{\sigma^2}\frown \chi^2_{(n-2)}\]

podendo assim serem feitos testes como

\[\begin{split}\begin{array}{l} H_0:~\sigma^2=0~~vs~~H_1:~\sigma^2>0 \quad\leftarrow\text{Teste à var. dos erros} \\ \end{array}\end{split}\]

valor esperado

Assim, segue que:

\[E[ Y_i | x_i] = \beta_0 + \beta_1 x_i\]

ou ainda

\[Y_i | x_i = \beta_0 + \beta_1 x_i + \epsilon_i \sim N(\beta_0 + \beta_1 x_i, \sigma^2), \quad i=1, \ldots, n\]

observação futura

(a ser descrito)