distribuição t de Student
Uma distribuição t de Student é usada em inferência estatística para populações normais quando a variância populacional, \(\sigma^2\), não é conhecida.
O símbolo que identifica esta família de distribuições é \(t_n\) em que n é um inteiro que indica os graus de liberdade (gl, ou df de «degrees of freedom»).

propriedades
Cada distribuição \(t_n\) é simétrica em torno de 0.
À medida que \(n \to + \infty\) a distribuição \(t_n\) aproxima-se da distribuição normal padrão, \(N(0,\; 1)\).
De momento, consulte mais detalhes na página wikipedia.
tabelas para a t de Student
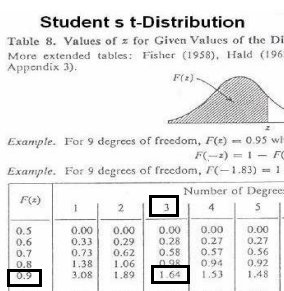
Problema. Pretende-se calcular \(P(T \ge 1.64)\) com \(T\) seguindo t de Student com 3 graus de liberdade (3 «degree of freedom» ou df em alguma calculadoras).
Resolução. Como pode ser visto na tabela, na imagem linha «0.9» e coluna «3», a área (i.e., a probabilidade) para a esquerda de \(t_{obs}=1.64\), com 3 graus de liberdade é 0.9.
Assim, a área para a direita de \(t_{obs}=1.64\) é 1 - 0.9 = 0.1, isto é, \(P(T \ge 1.64)=0.1\)
Duas notas:
Por convenção, nesta tabela, é a àrea à esquerda que está definida. Se for para a direita, temos que fazer «1 - área_esquerda».
Claro que há uma limitação: para valores de \(t_{obs}\) que não estejam listados torna-se necessário arredondar, interpolar ou usar valores próximos, quando não há recurso a software apropriado.
R Project
Inversa da t-Student
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
Pretende-se determinar q tal que P(T <= q) = 0.975
qt(0.975, 31)
copie o comando e coloque aqui
Excel para t de Student
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
Excel em português:
=DIST.T(2,1; 9; VERDADEIRO) determina P(T <= 2.1) sendo \(T \sim t_{9}\) (deve dar 0,967440859)
=INV.T(0,025; 9) determina q tal que P(T <= q) = 0.025 sendo \(T \sim t_{9}\) (deve dar -2,262157163)
=INV.T(0,975; 9) determina q tal que P(T <= q) = 0.975 sendo \(T \sim t_{9}\) (deve dar 2,262157163)
Consulte, também, ficheiros Excel já preparados.
texas TI Nspire CX
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
inversa: obter o quantil dada a área
Problema: saber q tal que P(T <= q) = 0.975.
MENU:
6: Estatística
5: Distribuições
9: Inversa da T
area = 0.975; graus de liberdade (df)=31;
O resultado deve ser 2,039513446.
probabilidade: obter a área dado o quantil
Problema: P(T <= 2) = ?
MENU:
6: Estatística
5: Distribuições
9: Distribuição T de Student
x = 2
graus de liberdade (df)=31;
O resultado deve ser 0,972836392.
texas TI 84
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
(por fazer)
casio FX 9860gii
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
Aviso: esta calculadora determina o valor q dando «a probabilidade para a frente» de q.
Inversa: P(T <= q) = 0.975 então q = ?
Estatística (2) => DIST (F5) => T (?) => InvT (?) => data=variable; area=0.025; df=31; o resultado deve ser 2,039513446.
Distribuição: P(T <= 2,039513446) = ?
(confirmar) Estatística (2) => DIST (F5) => T (?) => TcD (?) => data=variable; x=2,0395; df=31; o resultado deve ser 0.975.
casio FX CG 20
Exemplo:
\(T \sim t_{31}\) em que \(t_{31}\) é uma distribuição t-Student com 31 graus de liberdade (degrees of freedom=df=31)
Aviso: esta calculadora determina o valor q dando «a probabilidade para a frente» de q.
Inversa: P(T <= q) = 0.975 então q = ?
Estatística (2) => DIST (F5) => T (?) => InvT (?) => data=variable; area=0.025; df=31; o resultado deve ser 2,039513446.
Distribuição: P(T <= 2,039513446) = ?
(confirmar) Estatística (2) => DIST (F5) => T (?) => TcD (?) => data=variable; x=2,0395; df=31; o resultado deve ser 0.975.
tabela para a t de Student
Baixe as tabelas aqui tabelas.
As tabelas são intuitivas porém, quando não existe o valor pedido é necessário fazer interpoolação.
Exemplo de interpolação:
Exemplo: \(T \sim t_{31}\), distribuição qui-quadrado com 31 graus de liberdade (degrees of freedom=df=31).
Para obter q tal que P(T <= q) = 0.975 verifica-se que
A tabela só tem 30 g.l. e 40 g.l. mas pretende-se 31 graus de liberdade (g.l.).
Em 0.975 obtemos os quantis 2.04 e 2.02 para 30 e 40 g.l., respectivamente.
A tabela tem esta informação e t é o quantil procurado:
30 |
31 |
40 |
|
2.04 |
t=? |
2.02 |
|
e, por igualdade de declives,
e obtém-se uma aproximação: \(t \approx = 2.038\).