ex. 5.10 (*)
Considere o ficheiro rolhas.csv que contém os valores de várias variáveis medidas num conjunto de 150 rolhas. Pretende-se estabelecer um modelo de regressão linear simples entre o perímetro total dos defeitos das rolhas (y) e a área total desses mesmos defeitos (x).
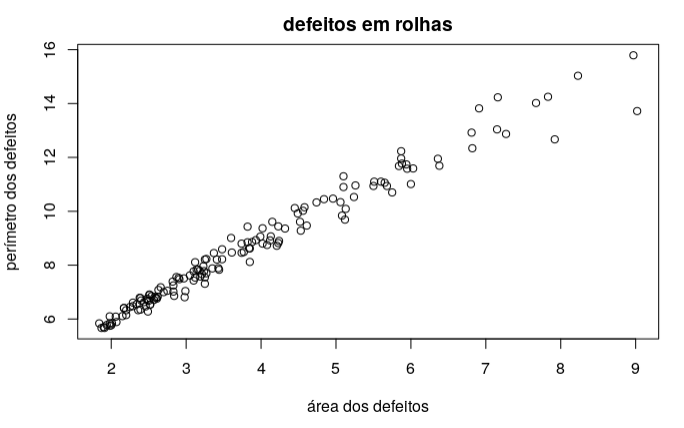
Considere o seguinte gráfico de dispersão
e a seguinte tabela de coeficiente (incompleta):
Estimate |
Std. Error |
t value |
Pr(\(>|t|\)) |
|
(Intercept) |
3.33553 |
0.08202 |
40.67 |
\(<2e-16\) |
ARM |
1.37780 |
0.01951 |
70.64 |
(valor-p) |
Residual standard error: 0.3877 on 148 degrees of freedom
Multiple R-squared: 0.9712, Adjusted R-squared: 0.971
F-statistic: 4989 on 1 and 148 DF, p-value: < 2.2e-16
(a) Comente o gráfico de dispersão.
☞ sugestões
☞ solução
O par de observações apresenta uma boa correlação linear.
(b) Escreva a reta de regressão.
☞ sugestões
☞ proposta de resolução
A coluna «Estimate» da tabela acima mostra as estimativas dos coeficientes:
\(\hat \beta_0 = 3.33553\) (ordenada na origem)
\(\hat \beta_1 = 1.37780\) (declive)
A reta estimada é \(\hat y=3.33553 + 1.37780 \, x\).
(c) O valor do coeficiente de declive é significativamente diferente de 0? Realize o cálculo do valor-p primeiro sem recurso aos dados (apenas com os dados da tabela) e depois com recurso aos dados (via software). Considere o nível de significância 5%.
(c-i) Escreva as hipóteses em causa indique a interpretação de cada uma no contexto da regressão linear.
☞ sugestões
☞ proposta de resolução
O declive é o coeficiente \(\beta_1\):
\(H_0: \beta_1=0\) vs \(H_1: \beta_1 \neq 0\)
Há uma interpretação especial no caso da regressão para estas duas hipóteses:
se H0 for favorável diz-se que a «regressão não faz sentido», isto é, não faz sentido explicar Y com base em x.
se H1 for favorável diz-se que a regressão faz sentido.
(c-ii) Calcule o valor-p do teste (em falta na tabela).
☞ sugestões
O teste t realiza-se de forma semelhante ao teste e intervalo t para a média com duas diferenças:
os graus de liberdade, df, são df=n-2 = 150-2;
o valor «Std. Error» da tabela já é o valor do desvio padrão de \(\hat \beta_1\) não sendo por isso necessário dividir por \(\sqrt{n}\).
☞ proposta de resolução
Na tabela do enunciado, «t value» é o valor observado da estatística de teste sob \(H_0: \beta_1=0\) e este «0» é usado em baixo.
O valor 70.64 que consta na segunda linha da tabela pode ser obtido assim:
Como \(t_{obs}|H0\) segue \(t_{n-2}\) então o valor-p, bilateral, é dado por:
valor-p = 2 CDF.t(70.64, +infinito, df=150-2) = 0.0
Notas: foram considerados n=150 pares (x,y).
(c-iii) Conclua.
☞ proposta de resolução
Rejeita-se \(H_0\). No contexto do problema significa que o perímetro total esperado dos defeitos das rolhas é significativamente influenciado pela área total desses mesmos defeitos.
(d) Forneça intervalos de confiança a 95% para os coeficientes de regressão.
☞ sugestões
O método é análogo ao T Interval com duas diferenças numéricas:
os graus de liberdade, df, são \(df = n - 2 = 150-2 = 148\);
o valor «Std. Error» da tabela já é o valor do desvio padrão de \(\hat \beta_1\) não sendo por isso necessário dividir por \(\sqrt{n}\).
☞ proposta de resolução
Pode determinar-se os ICs com base na informação da tabela considerado as expressões para cada um dos coeficientes:
Fazendo as devidas substituições, com \(t_{1-\alpha/2,n-2} = 1.976122\),
\(IC_{95\%}(b_0) = [3.173447, \;3.497606]\)
\(IC_{95\%}(b_1) = [1.339251, \;1.416343]\)
qt(0.975, 148)
[1] 1.976122
(e) Avalie a qualidade da regressão utilizando o coeficiente de determinação.
☞ sugestões
☞ solução
\(R^2 = 0.9712\) que é superior a 0.9 confirmando a boa qualidade obtida no gráfico de dispersão.
(f) Qual a percentagem de variabilidade de Y explicada por X?
☞ sugestões
☞ solução
97.12% de variabilidade de Y explicada por X: o perímetro total dos defeitos das rolhas (y) é explicado em 97% pela área total desses mesmos defeitos (x).