ex. 5.9
NNa indústria da madeira é usual transacionar a madeira de acordo com o seu volume. A madeira é submersa em água e o seu volume é medido através da variação do nível da água. No entanto, este processo de medição não pode ser aplicado diretamente na floresta e só é aplicável a árvores já abatidas. Uma forma de avaliar o volume das árvores é através do seu diâmetro, que é fácil de medir. O ficheiro arvores.csv contém medições do diâmetro e do volume de um conjunto de 32 árvores apresentando o seguinte diagrama de dispersão:
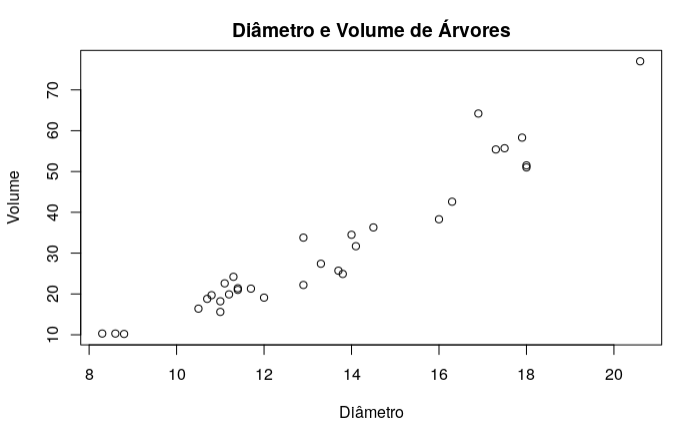
(a) Indique o coeficiente de correlação amostral entre o diâmetro e o volume.
Pearson's product-moment correlation
data: dados$DIAMETRO and dados$VOLUME
t = 18.491, df = 30, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.9165703 0.9799006
sample estimates:
cor 0.9588222
☞ sugestões
A reflectir.
☞ solução
r = 0.9588222 (próximo de 1; correlação forte positiva).
(b) Parece-lhe adequado utilizar um modelo de regressão linear simples para exprimir a variável volume em função do diâmetro?
☞ sugestões
A reflectir.
☞ solução
Observa-se adequado ajustamento dos ponto a uma reta.
(c) Especifique o modelo teórico de regressão linear simples, exprimindo os volumes (y) como função dos diâmetros (x) das árvores.
☞ sugestões
A reflectir.
☞ solução
\(Y = \beta_0 + \beta_1 x + \epsilon\), em que \(\epsilon_i\sim N(0, \sigma^2)\) sendo \(\sigma^2\) a variância dos erros.
(d) Com base nos dados disponíveis na tabela seguinte quais são os valores estimados para os parâmetros da regressão?
Residuals:
Min |
1Q |
Median |
3Q |
Max |
-8.6461 |
-3.6578 |
0.0203 |
3.2254 |
14.3895 |
Coefficients:
Estimate |
Std. Error |
t value |
Pr(\(>|t|\)) |
|
(Intercept) |
-38.8564 |
3.8914 |
-9.985 |
4.74e-11 |
DIAMETRO |
5.2466 |
0.2837 |
18.491 |
\(<\) 2e-16 |
Residual standard error: 4.981 on 30 degrees of freedom
Multiple R-squared: 0.9193, Adjusted R-squared: 0.9167
F-statistic: 341.9 on 1 and 30 DF, p-value: < 2.2e-16
☞ sugestões
A reflectir.
☞ solução
\(\hat{b}_0 = -38.856,\ \hat{b}_1 = 5.247\)
(e) Qual é a equação da reta de regressão?
☞ sugestões
A reflectir.
☞ solução
\(y = -38.856 + 5.247 x\)
(f) Avalie a qualidade e significado da regressão utilizando:
(f-i) O gráfico de dispersão
☞ sugestões
A reflectir.
☞ solução
(ainda sem gráfico)
(f-ii) O coeficiente de determinação
☞ sugestões
A reflectir.
☞ solução
\(R^2 = 0.919\) (superior a 0.9)
(f-iii) O teste ao declive (\(\alpha=0.05\))
☞ sugestões
A reflectir.
☞ solução
\(H_0: b_1 = 0\) vs \(H_1: b_1 \neq 0\), valor \(p = 0.0 < \alpha\), rejeita-se \(H_0\)
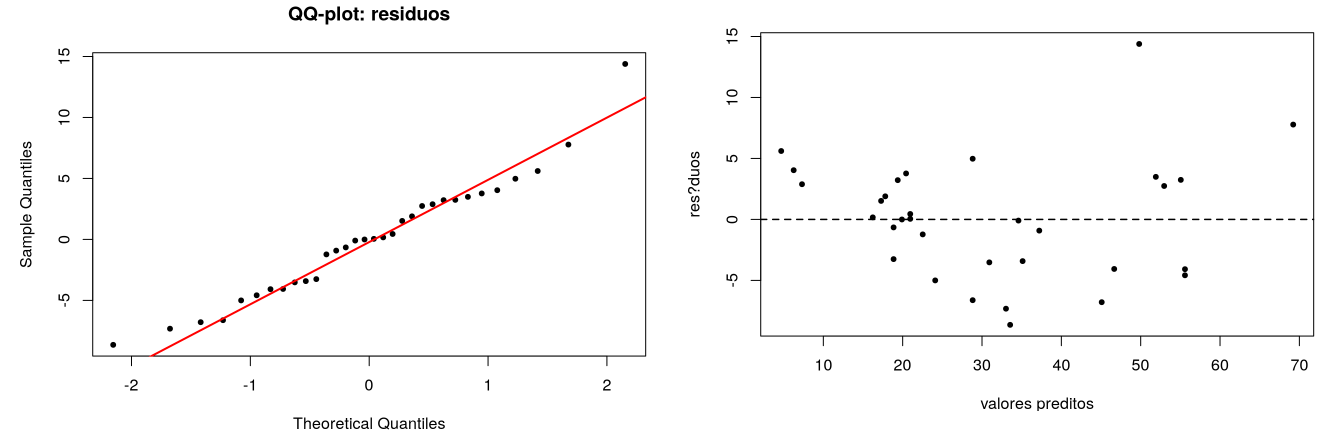
(g) Efetue, com base na informação seguinte, uma análise de resíduos para validar os pressupostos de realização de uma análise de regressão linear.
Shapiro-Wilk normality test
data: residuals(modelo)
W = 0.96431, p-value = 0.3587
☞ sugestões
A reflectir.
☞ solução
Observa-se pelo QQ-plot dos resíduos que os pontos ficam próximos da reta o que valida o pressuposto da normalidade dos resíduos.
Pelo gráfico dos resíduos versus valores preditos observa-se também a independência dos erros, uma vez que os pontos se encontram aleatoriamente dispersos em torno do eixo xx.