ex. 5.11
Recolheu-se informação relativa ao número de fogos florestais e área ardida (em hectares) em Portugal, desde 1943 até 1978 fogos.csv.
Pretende-se relacionar a área total ardida com o número de fogos.
(a) Construiu-se um diagrama de dispersão das duas variáveis
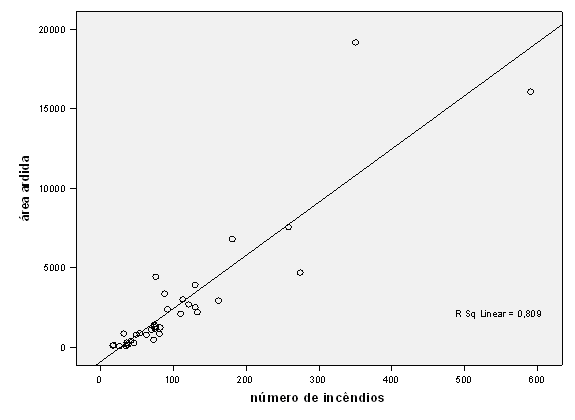
(a-i) Acha que se pode observar uma relação linear subjacente aos dados?
☞ sugestões
a refletir
☞ solução
A observação do gráfico não sugere adequação de um modelo linear.
(a-ii) O que pode dizer sobre a variabilidade dos dados?
☞ sugestões
a refletir
☞ solução
À medida que os valores de \(x\) aumenta, aumenta a dispersão dos valores de \(y\); O gráfico sugere efetuar uma transformação da variável \(y\) (nomeadamente, de tipo logarítmica).
(b) Qual o valor do coeficiente de determinação?

☞ sugestões
A reflectir.
☞ solução
- \(R^2 = 0.809\), menor que 0.9, o que sugere que a relação
entre math:y e math:x pode não ser bem modelada por uma regressão linear simples.
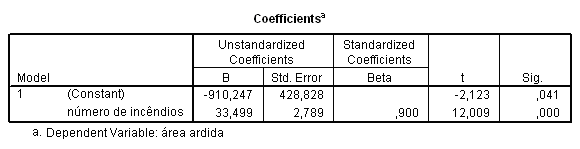
(c) Com base na tabela de regressão indique a equação da reta de regressão.
☞ sugestões
A reflectir.
☞ solução
\(y=-910.247 + 33.499x\)
(d) Por cada incêndio adicional que se observe, qual é a área média que se espera que arda?
☞ sugestões
A reflectir.
☞ solução
\(\hat{\beta}_1 = 33.499\)
(e) Teste se a ordenada na origem é significativamente diferente de 0, ao nível de signific^{a}ncia \(1\%\).
(e-i) Escreva as hipóteses em causa.
☞ sugestões
A reflectir.
☞ solução
\(H_0: \beta_0 = 0\) vs \(H_1: \beta_0 \neq 0\)
(e-ii) Registe o valor-p do teste.
☞ sugestões
A reflectir.
☞ solução
valor-p = 0.041
(e-iii) Conclua.
☞ sugestões
A reflectir.
☞ solução
valor-p superior a \(\alpha = 0.01\). Assim, não se rejeita \(H_0\); Logo, sob a validade do modelo de regressão linear, é esperada que a área ardida seja (significativamente) nula quando não se observam incêndios!
(f) Teste se o declive é significativamente diferente de 0, ao nível de signific^{a}ncia $1%$.
(f-i) Escreva as hipóteses em causa.
☞ sugestões
A reflectir.
☞ solução
\(H_0: \beta_1 = 0\) vs \(H_1: \beta_1 \neq 0\)
(f-ii) Registe o valor-p do teste.
☞ sugestões
A reflectir.
☞ solução
valor-p = 0.0
(f-iii) Conclua.
☞ sugestões
A reflectir.
☞ solução
valor-p inferior a \(\alpha = 0.01\). Assim, rejeita-se \(H_0\). Logo, sob a validade do modelo de regressão linear, é esperada que a área ardida seja (significativamente) afectada pelo número de incêndios!
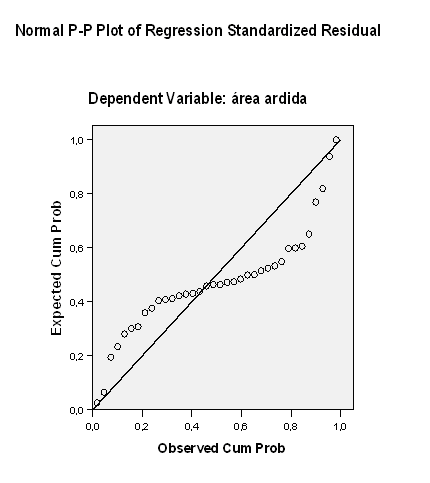
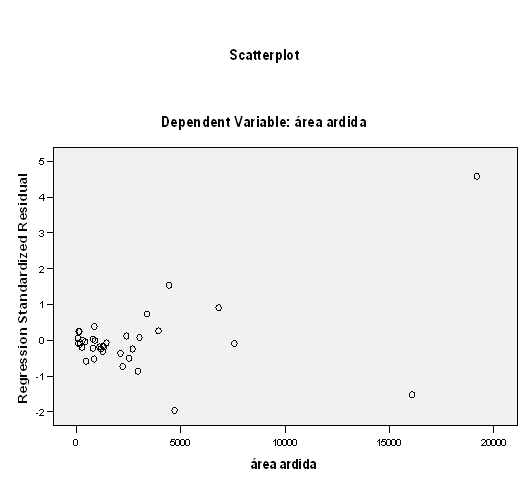
(g) Com base nos seguintes gráficos efetue uma análise de resíduos para averiguar se pode considerar válidos os pressupostos da análise de regressão linear.
☞ sugestões
A reflectir.
☞ solução
- Gráfico 1: os pontos não apresentam uma distribuição
aleatória em torno da reta \(y=x\)
Gráfico 2: os pontos não apresentam o mesmo tipo de dispersão em torno do eixo do \(xx\) (reta horizontal passando pelo ordenada nula).
Estes dois gráficos colocam em causa a validade dos pressupostos de regressão. Portanto, todas as conclusão obtidas sob a validade do modelo de regressão podem não estar corretas.