ex. 5.8 (*)
Uma equipa de investigadores, ao abordar o estudo de bases moleculares do envelhecimento, investigou também a possibilidade de que as dietas hipocalóricas prolonguem o tempo de vida. Para o efeito, usaram 9 ratos (Mus minutoides) de uma mesma ninhada que são separados e colocados em gaiolas individuais em ambientes similares, mas com dietas diferentes. Na tabela, encontram-se as Kcal, (x, fornecidas diariamente aos ratos (depois de desmamados e separados) e os respectivos tempos de vida, (y), também em unidades convencionais de 360 dias.
Use a calculadora ou software para responder às seguintes questões.
Calorias |
Tempo |
12.43 |
0.049 |
13.52 |
0.064 |
14.42 |
0.059 |
15.24 |
0.051 |
16.06 |
0.073 |
16.88 |
0.095 |
17.70 |
0.245 |
17.84 |
0.222 |
18.76 |
0.350 |
(a) Construa um diagrama de dispersão para visualizar a relação entre as variáveis e comente.
☞ proposta de resolução
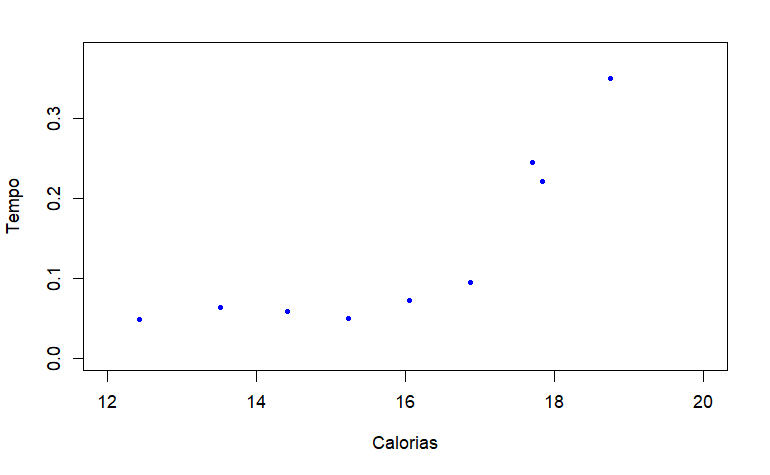
O diagrama de dispersão apresenta uma correlação, em média, monótona crescente mas não linear. Como são poucas observações, também não se rejeita já a ideia de uma correlação mesmo linear. (No entanto, vão usar-se estes dados para estudo da regressão linear simples, o tema principal do capítulo).
Como extra, verifica-se que o coeficiente de Spearman (e o seu valor-p) sugerem mais uma correção não linear pois a estimativa de Spearman é 0.9167 (boa correção monótona) e de Pearson é 0.839 (abaixo de 0.90 de uma boa linearidade).
Spearman's rank correlation rho
data: dados$Calorias and dados$Tempo
S = 10, p-value = 0.001312
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.9166667
Pearson's product-moment correlation
data: dados$Calorias and dados$Tempo
t = 4.0141, df = 7, p-value = 0.005098
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.3834512 0.9643374
sample estimates:
cor
0.8349468
As calculadoras estimam o coeficiente de determinação r^2 que é R^2=0.695, ou seja, apenas 70% da variabilidade de Y é explicada pela variabilidade em x. É pouco para uma regressão pois o diagrama de dispersão mostra uma curva e não tanto uma reta.
(b) Escreva o modelo teórico de regressão linear simples, exprimindo os tempos de sobrevivência (y) como função da quantidade diária de calorias (x) fornecida na dieta dos ratos.
☞ sugestões
☞ proposta de resolução
Usando a notação semelhante à documentação:
\(Y_i = b_0+b_1 x_i + \epsilon_i\)
que quer dizer que um modelo matemático de regressão linear é obtido por uma reta (média) \(b_0 + b_1 ` e a esta reta são somados "erros" aleatórios :math:\)epsilon_i` modelados, neste modelo matemático, por uma distribuiçãO normal centrada em zero (o habitual nos erros), e com desvio-padrão \(\sigma\) (ou variância \(\sigma^2\)).
\(Y_i\) é uma v.a. que dá o Tempo de vida;
\(x_i\) é um valor independente que indica as Calorias consumidas.
(c) Quais são os valores estimados para os parâmetros da regressão?
☞ sugestões
calculadoras gráficas (use «LinRegTTest» e não outras modalidades de regressão das calculadoras)
☞ solução
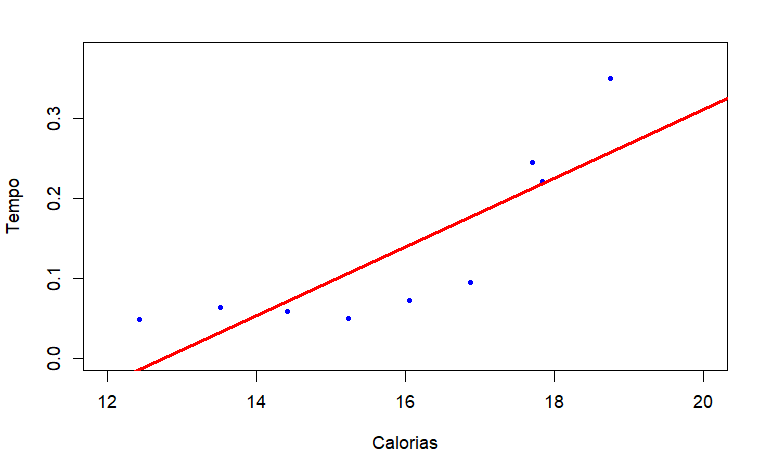
estimativa da ordenada na origem: \(\hat \beta_0 = \hat b_0 = -0.54761\); esta estimativa tem que ser negativa pois a reta estimada cruza o eixo YY abaixo de zero;
estimativa do declive: \(\hat \beta_1 = \hat{b}_1 = 0.04296\); este declive nunca é um valor muito elevado, pois o declive usando as coordenadas extremas no gráfico seria \((0.3 - 0.0)/(20-0)\), i.e., muito pequeno.
Erros: no modelo existe uma v.a. \(\epsilon\). Sendo uma v.a. não tem um valor mas representa todos os erros numa amostra que se designam por resíduos: \(e_i = y_i - \hat y\) para um dado \(x_i\). O que pode ser estimado é o desvio padrão dos erros, já que estes são modelados por uma v.a. Normal de média 0 e variância \(\sigma^2\).
Em algumas calculadoras é a letra «s» que o estima: \(\hat \sigma = s\). No entanto, os parâmetros da regressão são apenas \(\beta_0\) e \(\beta_1\).
(d) Qual é a equação da reta de regressão? Faça um esboço do gráfico.
☞ sugestões
Basta usar os coeficientes da alínea anterior: y=mx+b
Para traçar a reta, deve marcar dois pontos, naturalmente.
A equação de reta não tem erro, é mesmo só a equação de uma reta. Veja a resposta anterior.
☞ proposta de resolução
(e) Comente o valor estimado para a ordenada na origem? Tem algum sentido particular no contexto do problema?
☞ sugestões
Sem calorias ingeridas (calorias=0) qual o tempo de vida?
☞ solução
A reta só faz sentido na zona em que as calorias ingeridas permitem o bom desempenho corporal. Se forem abaixo dum certo limiar não faz sentido dizer que a esperança de vida é maior. Neste sentido, os dados fornecidos não apresentam o caso se subnutrição.
(f) Teste se o declive é significativamente diferente de 0, ao nível de significância \(1\%\). Com base nesse teste o que pode concluir quanto ao tipo de dieta alterar o tempo de vida dos ratos.
(f-i) Escreva as hipóteses em causa.
☞ sugestões
A estatística a usar para a inferência sobre o declive usa a distribuição t de Student.
Consulte: inferência da regressão
☞ proposta de resolução
\(H_0: \beta_1 = 0\) vs \(H_1: \beta_1 \neq 0\)
A calculadora apresenta valor-p para este teste.
(f-ii) Registe o valor-p do teste.
☞ sugestões
☞ solução
valor-p = 0.00509
A estatística de teste, na calculadora, costuma surgir na letra «t=…»
Também pode ser obtido por: 2xCDF.T(….) a partir desse valor t.
(f-iii) Conclua.
☞ sugestões
É a usual conclusão.
☞ proposta de resolução
Como o valor-p é menor que \(\alpha = 0.01\) rejeita-se H0 (o declive da reta de regressão é significativamente diferente de zero, ao nível de significância de 1%).
Nesta situação, a expressão a usar é «a regressão faz sentido», isto é, em média, o valor de y depende do valor de x. Quando não há regressão, conhecendo x, nada se pode dizer de um valor médio para y.
(g) Teste se o declive é negativo, ao nível de significância 1% Com base nesse teste é de crer que as dietas hipocalóricas prolongam o tempo de vida dos ratos?
(g-i) Escreva as hipóteses em causa.
☞ sugestões
As calculadoras têm a possibilidade de escolha do tipo de teste: unilateral à esquerda, unilateral à direita e bilateral.
☞ proposta de resolução
\(H_0: \beta_1 = 0\) vs \(H_1: \beta_1 <0\).
(g-ii) Registe o valor do valor-p do teste.
☞ sugestões
O valor da estatística de teste é o mesmo porque a amostra é a mesma.
O que agora varia é o tipo de teste (unilateral esquerdo): só se calcula a área à esquerda.
☞ proposta de resolução
valor-p unilateral à esquerda = 0.0002….
Uma técnica, sem calculadora, pode ser esta guia para a conversão de p-values que conduz a dividir 0.00509 por 2.
(g-iii) Conclua.
☞ sugestões
A conclusão usual.
☞ proposta de resolução
Como \(p < \alpha = 0.01\) rejeita-se H0 (a reta de regressão apresenta um declive significativamente negativo, ao nível de significância 1%).
Portanto, é de crer que as dietas hipocalóricas prolongam o tempo de vida dos ratos.
(h) Que alteração média no tempo de vida dos ratos é produzida pela ingestão de mais 1 Kcal diariamente?
☞ sugestões
Uma analogia para ajudar a reflectir: um trabalho em «part-time» resulta na sua poupança média que é dada pela relação:
poupança = 120 euros x Mês + 1000 que já tinha, para Mês = 1,2,3,…
Que alteração média na poupança é ganha por trabalhar em part-time mais um mês?
☞ proposta de resolução
A alteração média, pela ingestão de mais 1 Kcal, é o próprio declive \(\hat{b}_1 = 0.04296\).