ex. 5.3
Um investigador pretende avaliar se uma dada balança está bem calibrada. Considerou 9 pesagens conhecidas \(x\) e determinou o respetivo peso atribuído pela balança \(y\). Os dados foram:
X |
2.0 |
2.0 |
2.0 |
4.0 |
4.0 |
4.0 |
6.0 |
6.0 |
6.0 |
Y |
2.1 |
1.8 |
1.9 |
4.5 |
4.2 |
4.0 |
6.2 |
6.0 |
6.5 |
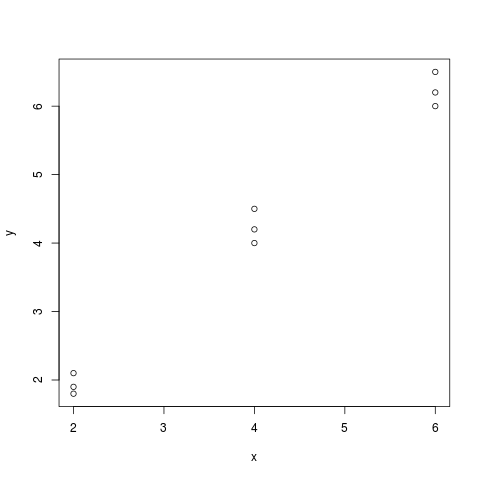
(a) Efetue um gráfico de dispersão.
☞ sugestões
Em R pode executar-se:
☞ solução
(b) Determine a equação da reta de regressão estimada.
☞ sugestões
Quando nada é dito, ou quando se pergunta se a «regressão faz sentido» então é melhor usar o «diferente» e só o valor-p é que depende dessa escolha. Os restantes valores na máquina não dependem do sinal escolhido.
☞ solução
\(y=-0.167+1.075x\)
(c) Calcule o coeficiente de determinação e comente.
☞ sugestões
☞ proposta de resolução
\(R^2=0.988\)
O investigador verificou que a relação entre o peso real e o peso atribuído pela balança é bem modelada por uma regressão linear simples já que o valor obtido para o coeficiente de determinação é elevado e o gráfico de dispersão apresenta uma relação linear
Pode afirmar-se, assumindo este modelo teórico de regressão linear, que
98.8% da variabilidade de Y é explicada pela variabilidade de x;
ao variar x, há uma variação em Y composta de duas influências:
a influência do x é 98.8%;
a influência dos erros é 1.2%.
Outros elementos faltam para validar a regressão e averiguar a qualidade da regressão.