ex. 5.2 (*)

Para averiguar a existência de relação entre a massa muscular de um adulto com a sua idade, um nutricionista recolheu uma amostra de 18 indivíduos, com idade entre 40 e 79 anos, e observou em cada um deles a idade (X) e a massa muscular (Y). Com os dados recolhidos obteve o seguinte diagrama de dispersão.

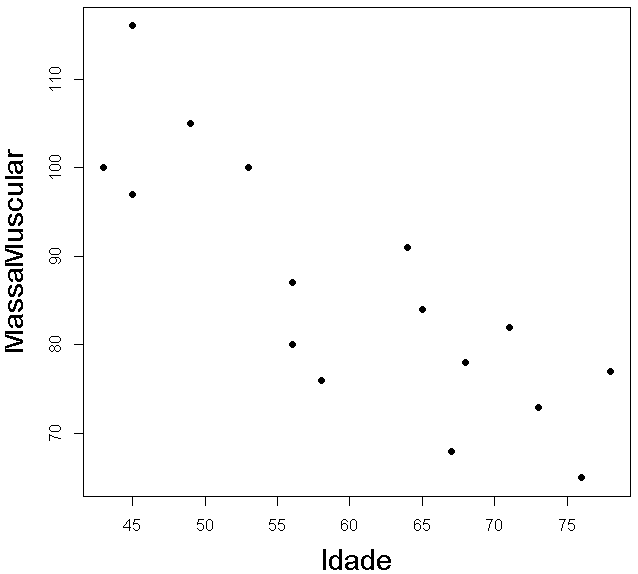
Avalie se cada frase tem sentido matemático e, se fizer, a veracidade desta.

☞ sugestões

Sugestão única de leitura: correlação.

(a) existe uma associação do tipo linear entre os 18 indivíduos e cada uma das variáveis (X e Y).

☞ proposta de resolução

Não tem sentido matemático. As palavras usadas na frase pertencem ao vocabulário do tema da correlação mas não fazem sentido. É necessário um par de observações e «um indivíduo» não é uma observação mas um elemento do qual se observam atributos.

(b) o coeficiente de correlação amostral de Pearson entre X e Y deve corresponder a um valor negativo indicando que os adultos mais novos tendem a ter menor massa muscular.

☞ proposta de resolução

A frase tem sentido matemático mas é falsa. A primeira patre é verdade: «o coeficiente de correlação amostral de Pearson entre X e Y deve corresponder a um valor negativo» mas atenção à segunda parte da frase: «adultos mais novos tendem a ter menor massa muscular».

(c) o valor do coeficiente de correlação amostral de Spearman

entre X e Y deve ser muito próximo de zero.

☞ proposta de resolução

A frase tem sentido matemático mas é falsa. Em caso de linearidade, o coeficiente de Spearman será sempre diferente de 0 (que apenas existe ordem nas observações que não precisam de ser numéricas).

(d) Um adulto mais velho tenderá a ter menor massa muscular.

☞ proposta de resolução

A frase tem sentido matemático e é verdadeira. Não diz mas ambos os coeficientes, de Pearson e de Spearman, vão apresentar coeficientes negativos.

FIM