ex. 5.4 (*)

Recolheram-se os valores do índice de Apgar medido ao fim de 1 e de 5 minutos num conjunto de recém-nascidos em hospitais portugueses, selecionados ao acaso. O índice de Apgar toma valores (inteiros) de 0 a 10 que resultam de uma classificação feita por médicos aos recém-nascidos. Esta classificação é distribuída por 5 atributos: frequência cardíaca, esforço respiratório, tónus muscular, irritabilidade reflexa e cor. Cada atributo é classificado com 0, 1 ou 2 e o índice resulta da soma das 5 classificações. Um bebé normal deve ter índice superior ou igual a 8. Os dados recolhidos encontram-se no ficheiro apgar.csv.

(a) Identifique variáveis $X$ e $Y$ e classifique-as quanto à sua natureza e escala.

☞ sugestões

A reflectir.

☞ proposta de resolução

• X = índice apgar ao final de 1 minuto;

• Y = índice apgar ao final de 5 minutos.

Ambas são variáveis quantitativas discretas na escala de intervalos.

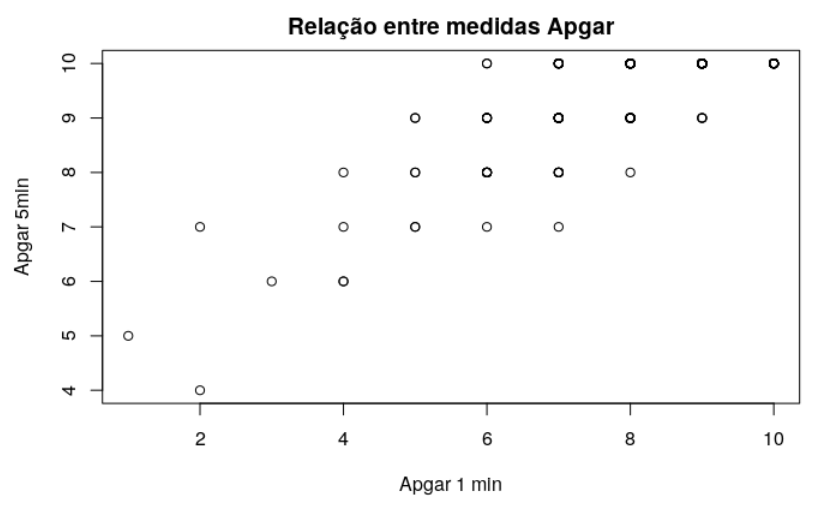
(b) Comente o gráfico de dispersão das duas variáveis.

☞ sugestões

☞ proposta de resolução

Verifica-se uma possível relação linear entre as variáveis com bastante dispersão. Note-se que os valores em (x) e (y) são inteiros e dão um aspeto de quadrícula ao gráfico.

(c) O que entende por existência de correlação entre duas variáveis?

☞ sugestões

A reflectir.

☞ proposta de resolução

Conhecendo o valor da variável x podemos saber o valor de y, tendo em conta que existem erros aleatórios na medição de y. Quando a correlação é monótona podemos inverter o papel de x e y: dado y podemos conhecer x, tendo em conta que existem erros aleatórios na medição de x. No caso de não ser monótona num dado domínio, podemos dividir o domínio, e verificar a propriedade anterior em secções.

(d) O que entende por inexistência de correlação entre duas variáveis?

☞ sugestões

A reflectir.

☞ proposta de resolução

No caso de não existir correlação diz-que se as variáveis não são correlacionadas. Não é possivel prever qualquer valor esperado (médio) para y com base num dado x, e vice versa.

(e) As variáveis são correlacionadas? Justifique devidamente a sua resposta apoiada no gráfico de dispersão e na seguinte tabela do R:

Pearson's product-moment correlation
data:  dados$Apgar1 and dados$Apgar5
t = 21.836, df = 221, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7799464 0.8641527
sample estimates:
cor 0.8266219

☞ sugestões

A reflectir.

☞ proposta de resolução

O coeficiente amostral de Pearson $r=0.8$ indica correlação moderada a forte. O valor-p confirma que a correlação é significativa. Em média, quando aumenta o índice «Apgar 1min» aumenta o índice «Apgar 5min».

(f) Com base na tabela, quantos pares de observações existem na amostra? O gráfico induz em erro?

☞ sugestões

A reflectir.

☞ proposta de resolução

O número de graus de liberdade, 221, indica que há $n=223$ pares observados. Como ocorre muita sobreposição, devido aos valores observados, parece que a amostra é mais pequena.