distribuição binomial
Trata-se de uma distribuição discreta cuja descrição de contagem é sempre com esta forma:
X = número de «sucessos» em n provas independentes
descrição
Trata-se de uma distribuição discreta cuja descrição de contagem é sempre com esta forma:
X = número de «sucessos» em \(n\) provas independentes
Um exemplo desta va é:
X = número de caras em 10 lançamentos de uma moeda
em que o «sucesso» é «sair cara» e o número de provas independentes é 10.
Diz-se que \(X\) segue uma distribuição Binomial de parâmetros:
\(n\) : o número de provas, ou experiências, independentes;
\(p\) : a probabilidade de sucesso em cada prova ou experiência.
A notação habitual é
que significa que a função massa de probabilidade é dada por
combinações
A expressão \(C_x^n\) designa combinações de n objectos agrupados x a x:
Por exemplo,
Se (a,b,c,d) são os objetos então combinados dois a dois têm-se as 6 combinações
(a,b), (a,c), (a,d), (b,c), (b,d), (c,d).
exemplos de binomiais
Exemplo 1. X = número de caras em 10 lançamentos de uma moeda
é uma contagem de sucessos em lançamentos de moedas
o sucesso é «sair cara»; sendo a moeda for equilibrada temos p=P(«sucesso»)=0.5
são realizados exatamente 10 lançamentos independentes
A notação matemática usada é:
e a expressão acima é uma maneira mais fácil de escrever \(f(x)=C^{10}_x 0.5^x (1-0.5)^{10-x}\), x=0,1,…,10.
Exemplo 2. X = número de defeitos em 35 peças de roupa avaliadas
é uma contagem de «sucessos» na análise de uma peça de roupa
o sucesso ocorre quando «a peça de roupa tem defeito» e considera-se p=P(roupa com defeito) (prob. desconhecida)
foram analisadas exatamente 35 peças de roupa (independentes)
sendo \(p\) a probabilidade de uma peça de roupa ser defeituosa;
Exemplo 3. X = número de praticantes de desporto no conjunto de 43 alunos presentes na sala de aula
é uma contagem de sucessos ao entrevistar cada estudante
o sucesso é «o estudante pratica desporto», considere-se p=P(o estudante pratica desporto)
foram entrevistados, exatamente, 43 estudantes
sendo \(p\) a probabilidade de um estudante praticar desporto
Exemplo 4. X = número de erros de medição superiores a 0.01mg em 100 pesagens realizadas
é uma contagem de sucessos ao fazer medições
o sucesso é «foi detetado um erro de medição superior a 0.01mg», considere-se p=P(erro de medição superior a 0.01mg)
foram revistas, exatamente, 100 pesagens
sendo \(p\) a probabilidade de se cometer um erro de medição superior a 0.01mg numa pesagem.
propriedades
média populacional ou número esperado
\(E[X]=np\)
Note que
o número esperado não precisa ser inteiro mesmo que a v.a. seja inteira.
Por exemplo, em Portugal houve 1.42 filhos por casal em 2019 e este valor serve de comparação com anos anteriores. Claro que ninguém vai ter 0.42 filhos e por isso a noção de média populacional é uma quantidade sem representação real. Assim, no cálculo \(np\) não se deve arredondar o número esperado a um número inteiro. Fonte: Indicadores de fecundidade.
variância populacional
\(Var[X]=np(1-p)\)
Exercício. Faça o gráfico de p(1-p). Para que valor de p é que a variância é máxima?
soma de duas variáveis binomiais
Sejam \(X\) e \(Y\) duas v.a.”s independentes tais que
Assim, nestas condições,
Exemplo.
Admita que a probabilidade de uma peça ser defeituosa é \(0.01\). Considere as variáveis
X = «número de peças defeituosas retiradas com reposição de um lote A de \(100\) peças»
e
Y = «número de peças defeituosas retiradas com reposição de um lote B de \(500\) peças».
Assim, \(X \sim B(100,0.01)\) e \(Y \sim B(500,0.01)\).
Então, \(Z=X+Y\) = «número de peças defeituosas no conjunto dos dois lotes» segue uma distribuição \(B(600,0.01)\).
R project
Exemplo. Determinar \(P(X \le 3)\) quando \(X\) segue uma \(Binomial(n=20, p=0.2)\):
pbinom(3,20,0.2)
[1] 0.4114489
Calculadoras gráficas
texas TI Nspire CX
determinar \(P(X = 3)\) quando \(X\) segue uma Binomial(n=20, p=0.2):
modo «calculadora»
Menu => estatística (6) => distribuições… (5) => função densidade binomial..
depois colocar o n=20, p=0.2, x=3
determinar \(P(X \le 3)\) quando \(X\) segue uma Binomial(n=20, p=0.2):
modo «calculadora»
Menu => estatística (6) => distribuições… (5) => função de distribuição binomial..
depois colocar n=20, p=0.2, limite inferior=0 e limite superior= 3
determinar \(P(X \ge 3)\) quando \(X\) segue uma Binomial(n=20, p=0.2):
modo «calculadora»
Menu => estatística (6) => distribuições… (5) => função de distribuição binomial..
depois colocar n=20, p=0.2, limite inferior=3 e limite superior=20 (pois x=0,1,…,20)
alternativa importante no caso discreto :
\(P(X \ge 3) = 1 - P(X \le 2)\) pois é uma va discreta
depois colocar n=20, p=0.2, limite inferior=0 e limite superior=2 e fazer «1 - resultado»
Baixe o manual da NSpire: TI-Nspire Reference Guide PT.
Esta máquina determina probabilidades da forma \(P(a \le X \le b)\) em que «a» e «b» são os limites inferior e superior do intervalo.
Contribuições:
Ana Madalena Garcia (2018/2019)
Ana Isabel Azevedo (2018/2019)
João Fonseca (2019/2020)
texas TI 84 e variantes
Indicações válidas para as variantes: TI 84 plus, TI 84 Plus C Silver Edition.
Exemplo: \(X\) segue uma Binomial(n=20, p=0.2):
\(P(X = 3)\)
Selecione as teclas 2nd, DISTR (VARS) para ter acesso ao menu de distribuição.
Selecionar A: binompdf e depois: binompdf(20, 0.2, 3)
- Por vezes surge um menu a pedir parâmetros:
botão DISTR-> opção binompdf-> (trials:20; p=0,2, x value= 3)
\(P(X \le 3)\):
Selecione as teclas 2nd– DISTR (VARS) para ter acesso ao menu de distribuição.
Selecionar B: binomcdf. Esta máquina calcula valores acumulativos da forma “inferiores a …” (\(P(X \le x)\)) e temos de fazer da seguinte forma: binomcdf(20, 0.2, 3)
- Por vezes surge um menu a pedir parâmetros:
botão DISTR-> opção binomcdf-> (trials:20; p=0.2; x value=3)
\(P(X \ge 3)\):
Nesta calculadora faz-se assim: \(P(X \ge 3) = 1 - P(X < 3) = 1 - P(X \le 2)\)
Então:
Escrever: 1- e depois
Selecione as teclas 2nd– DISTR (VARS).
Selecionar B: binomcdf e escrever binomcdf(20, 0.2, 2) (atenção à ordem)
Por vezes surge um menu a pedir parâmetros: - botão DISTR-> opção binomcdf-> (trials: 20; p: 0.2; x value: 2)
Faça clique na imagem para outros casos:

Contribuição original de Luana Filipe.
Contribuição adicional de Marta S. P. Mendes e Luís Filipe P. Borges
(estudantes de Bioestatística em 2018/2019).
casio FX 9860gii e similares
Exemplo: \(X\) segue uma Binomial(n=20, p=0.2):
Menu STAT; DIST (F5); BINM (F5);
P(X=3): Bpd (F1); Data: Variable; x=3; Numtrials=20; p=0.2
P(X<=3): Bcd (F2); Data: Variable; x=3; Numtrials=20; p=0.2
P(X>=3):
\(P(X \ge 3) = 1 - P(X \le 2)\) pois é uma va discreta
Bcd (F2); Data: Variable; x=2; Numtrials=20; p=0.2
anotar o resultado no papel;
no modo «math» fazer: 1 - (ver resultado anterior)
Contribuição original de André P. Ventura
(estudantes de Bioestatística em 2018/2019).
casio FX CG 20
Exemplo: \(X\) segue uma Binomial(n=20, p=0.2):
Menu STAT (estatistica); DIST (F5); BINOMIAL (F5);
P(X=3): Bpd (F1); Data: Variable; x=3; Numtrials=20; p=0.2
P(X<=3): Bcd (F2); Data: Variable; Lower=0; Upper=3; Numtrials=20; p=0.2
P(X>=3): Bcd (F2); Data: Variable; Lower=3; Upper=20; Numtrials=20; p=0.2
P(X>=3) alternativa importante no caso discreto :
\(P(X \ge 3) = 1 - P(X \le 2)\) pois é uma va discreta
Bcd (F2); Data: Variable; Lower=0; Upper=2; Numtrials=20; p=0.2, e fazer «1 - resultado»
Faça clique na imagem para ver os écrans:
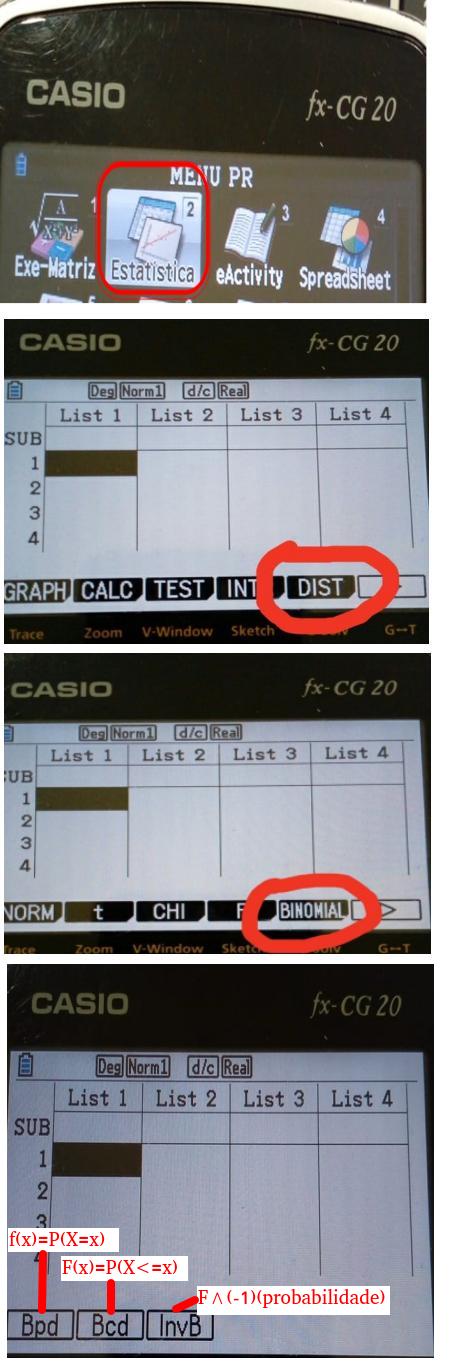
Contribuição original de Mara B. L. Gravato
Contribuição original com imagens de Ana Romariz
(estudantes de Bioestatística em 2018/2019).
Estas instruções dependem de marcas ou versões de calculadoras ou software
outros exemplos
Seja \(X \sim B(10,0.2)\). Assim, por exemplo,
\(P(X=4)=PDF.BINOM(4,10,0.2) \simeq 0.0881\)
\(P(X \geq 6)=1-P(X < 6) = 1-P(X \leq 5) = 1- F(5)\)
Logo, \(P(X \geq 6)= 1-CDF.BINOM$(5,10,0.2) \approx 0.0064\).
E, ainda,
\(E[4X-1]=4E[X]-1=4\times(10\times0.2)-1=7;\)
\(Var[4X-1]=16Var[X]=16\times(10\times0.2\times0.8)=25.6.\)