ajustamento à normal

São apresentadas ideias gerais sobre o conceito «ajustamento a uma distribuição» que é um sinónimo de «a amostra é bem modelada por uma dada distribuição».

necessidade de uma distribuição

De uma população é observado um atributo. Esse atributo é descrito por uma v.a., $X$, como, por exemplo, «X é o IMC de uma pessoa».

Assumimos que as condições (físicas, económicas, biológicas, etc) que deram origem à população estão estáveis no período de estudo. Nesse caso, é razoável pensar-se que a v.a. tenha uma distribuição de probabilidades associada, devido à estabilidade das condições. Conhecendo uma distribuição, pode-se responder ao cálculo de probabilidades, $F(x)=P(X \le x)$, e assim usar teorias da estatística matemática que assentam nessa função de distribuição $F(x)$ para realizar estatística inferencial por forma a conhecer melhor as características da população.

A imagem mostra como dados organizados em classes e colocados num histograma se podem assemelhar a uma função densidade $f(x)$:

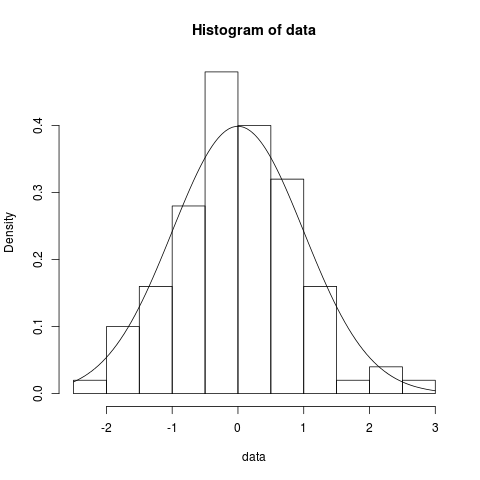
ajustamento da amostra à distribuição normal

A maior parte das técnicas de inferência realizadas nesta documentação têm como pressuposto que uma v.a. $X$ deve ser caracterizada por uma distribuição normal.

Com base numa amostra de dimensão n, como inferir que o atributo $X$, de uma populaçao, segue uma distribuição normal? Usando a notação de testes de hipóteses:

$$H_0\,:\, X \sim N(\mu,\sigma^2) \quad vs \quad H_1\,:\, X \text{ não segue } N(\mu,\sigma^2)$$

Para responder a esta questão, as técnicas apresentadas neste capítulo estão nos procedimentos para testar o ajustamento à normal.