ex. 5.17 (*)

Para avaliar a eventual existência de associação entre a dureza da água e a abundância de ninfas de Plecoptera, foram recolhidas amostras de água em diversos cursos de água. Os resultados encontram-se no ficheiro plecoptera.csv.

Realize um estudo completo de correlação entre as variáveis com os coeficientes de Pearson e de Spearman.

(A resolução do exercício requer comandos R ou excel não podendo ser realizado com a calculadora.)

☞ sugestões

correlação de Pearson

correlação de Spearman

☞ proposta de resolução

X = dureza da água (variável numa escala de razões);
Y = número de plecoptera (variável numa escala de razões);

O seguinte código em R realizar o diagrama de dispersão, determina os coeficientes amostrais e o valor-p dos testes associados.

dados <- read.csv("https://sweet.ua.pt/pedrocruz/dados/plecoptera.csv", sep=",", dec=".", header=TRUE)

# para visualizar a estrutura dos dados
str(dados)

# eliminar a primeira coluna pois é o ID do rio.
dados =dados[,-1]

# diagrama de dispersão
plot(dados, pch=20)

# Coeficiente amostral de Pearson e de Spearman
cor(dados$Dureza,dados$N_plecoptera, method = c("pearson"))
cor(dados$Dureza,dados$N_plecoptera, method = c("spearman"))

# Teste ao coeficiente populacional de Pearson e de Spearman
cor.test(dados$Dureza,dados$N_plecoptera,method = c("pearson"), conf.level = 0.95)
cor.test(dados$Dureza,dados$N_plecoptera,method = c("spearman"), conf.level = 0.95)

O gráfico de dispersão sugere uma curva média monótona descrescente.

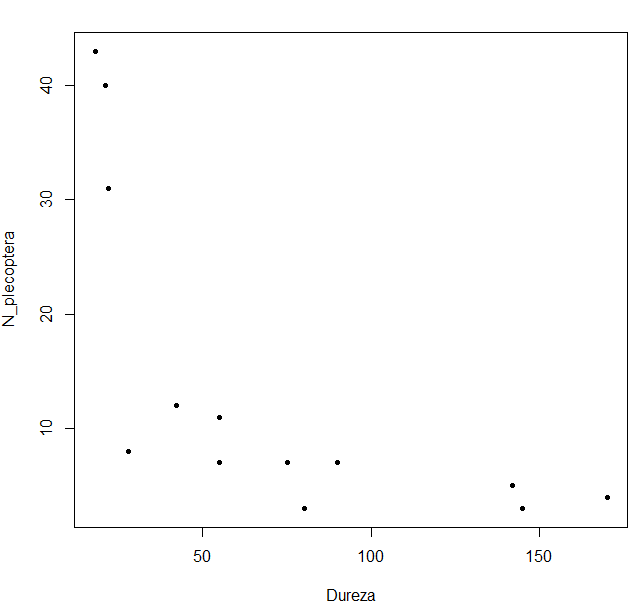
O coeficiente de Pearson não é o mais indicado para este tipo de configuração de pontos. Ainda assim tem um valor moderado \(r = -0.6728719\) e não se rejeitando que o coeficiente populacional, \(\rho\), seja significativamente diferente de zero (valor-p=0.01172):

Pearson's product-moment correlation

data:  dados$Dureza and dados$N_plecoptera
t = -3.0167, df = 11, p-value = 0.01172
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8928425 -0.1936990
sample estimates:
    cor
-0.6728719

O coeficiente de Spearman é o mais indicado para este tipo de configuração de pontos: curva média monótona decrescente apresentando uma correlação não monótona forte, \(r_s = -0.9141415\), e não se rejeitando que o coeficiente populacional, \(\rho_s\), seja significativamente diferente de zero (valor-p = 1.232e-05):

Spearman's rank correlation rho

data:  dados$Dureza and dados$N_plecoptera
S = 696.75, p-value = 1.232e-05
alternative hypothesis: true rho is not equal to 0
sample estimates:
    rho
-0.9141415

Interpretação: o diagrama de dispersão ilustra uma associação definida por uma função monótona não do tipo linear. Assim, o melhor coeficiente que traduz o tipo de associação entre as duas variáveis não será o de Pearson mas sim o de Spearman. O valor para o coeficiente de Spearman (-0.914) indica a existência uma associação forte negativa, definida por uma função monótona decrescente, estatisticamente significativa (valor-p= 0.00001232).

Conclusão: Existe maior abundância de plecoptera em cursos de água com baixa dureza.

FIM