ex. 3.6 (*)
Foi recolhida uma amostra de 32 árvores arvores.csv que contém o diâmetro, altura e volume de cada árvore. Para este enunciado considere apenas a amostra de alturas.
A seguir, apresentam-se os resultados obtidos com o recurso ao R.
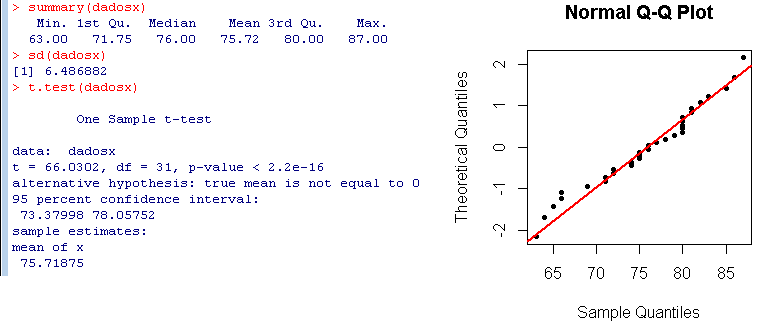
(a) Indique um intervalo de confiança a 95% para a altura média através da expressão mais apropriada do IC e depois, confirmando atráves da informação exposta, assumindo a normalidade dos dados.
☞ sugestões
O que significa «normalidade dos dados»?
consulte guia de procedimentos
☞ proposta de resolução
A variável aleatória é:
X = altura de uma árvore
A expressão «assumindo a normalidade dos dados», no contexto da alínea, é o mesmo que perguntar «Qual a distribuição da v.a. X?»:
X segue \(Normal(\mu, \sigma^2)\)
Na imagem, no corpo do enunciado, tem-se que:
sd(dadosx)= desvio padrão corrigido da amostra «dadosx», em que «sd» é standard deviation.
Assim, a variância amostral é conhecida calculando «(sd)^2».
Note-se que o parâmetro populacional \(\sigma\) não é fornecido no enunciado e portanto, tem-se que usar o «T Interval» (ver teste e intervalo t para a média):
Nas calculadoras deve procurar-se «INTR» ou «T INTR». Por exemplo, TI84: Stat => Tests => T Interval => depois
LIST: fornecer a amostra (agrupada ou não)
Variable: fornecer \(\bar x\) e \(s_c\) (desvio corrigido)
Para fazer com recurso à fórmula do IC, para o T Interval,
\(\bar x = 75.72\) (ver na imagem onde diz «mean»)
\(s_c= sd(dadosx) = 6.486882\) (ver quadro onde diz «sd(dadosx)»)
n = 32
Para obter o quantil \(t_{1-\alpha/2,n-1}\):
n - 1 = 31 graus de liberdade (degrees of freedom)
\(1 - \alpha/2= 0.975\)
grau de confiança: \(1 - \alpha=0.95\)
2.5%(esquerda) 95%(centro) 2.5%(direito) = 100%
TPC: com 90% quanto é \(1 - \alpha/2\)?
Com calculadora:
DISTR => inv.t(0.975, 31) = 2.039513
Com R project:
> qt(0.975, 31)
[1] 2.039513
IC(\(\mu\)) = [ 75.72 - 2.039513 * 6.486882 / sqrt(32) , 75.72 + 2.039513 * 6.486882 / sqrt(32) ] = [73.38123, 78.05877]
> 75.72 - 2.039513 * 6.486882 / sqrt(32)
> [1] 73.38123
> 75.72 + 2.039513 * 6.486882 / sqrt(32)
> [1] 78.05877
É aceitável caracterizar a altura de uma árvore com uma média no intervalo [73.38123, 78.05877] com base na mostra dada e grau de confiança 95%.
\(IC_{95\%}(\mu) = (73.3800,78.0575)\)
(b) Determine um intervalo de confiança a 95% para o desvio padrão da população assumindo a normalidade dos dados.
☞ sugestões
Consulte distribuição qui quadrado.
Consulte TH e IC do qui-quadrado para a variância.
Primeiro calcula-se o IC para a variância, depois usa-se a raiz quadrada sobre o intervalo.
☞ proposta de resolução
\(IC( \sigma ) = \sqrt{ IC(\sigma^2)}\)
\(\chi^2_n\) família de distribuições do qui quadrado (chi square), que depende do grau de liberdade n (degree of freedom)
\(1-\alpha/2\)
n-1 identifica qual a distribuição do qui quadrado
n -1 = 31 (pois são 32 árvores na amostra)
\(s_c^2= sd^2=6.48682^2\) (variância amostral corrigida)
Para calcular o quantil qui-quadrado consulte distribuição qui quadrado e as notas:
A notação \({\cal X}^2\) é um símbolo como um todo.
\(1 - \alpha = 0.95\)
\(1 - \alpha/2= 0.975\)
\(\alpha/2=0.025\)
O grau de confiança pedido é 95% e então \(1 - \alpha=0.95\). Esta é a probabilidade que é colocada no centro da \({\cal X}^2_{n-1}\) obtendo:
2.5%(à esquerda) 95%(ao centro) 2.5%(à direita)
Calculadoras como CASIO CG 20 e a TI nspire:
«qui quadrado» é «CHI SQ» em algumas calculadoras.
inv.chisq(0.025, 31)
inv.chisq(0.975, 31)
A TI 84 não tem e então pode usar-se o Excel para qui-quadrado (ver também excel):
=INV.CHIQ(0,975; 31) e =INV.CHIQ(0,0025; 31)
ou ainda o sistema R, recordando que «q» designa quantil e «chisq» designa «qui quadrado»:
> qchisq(0.025,31)
[1] 17.53874
> qchisq(0.975,31)
[1] 48.23189
Finalmente, a raiz quadrada, para se obter um IC para o desvio padrão:
(c) Qual o erro padrão (i.e. \(s_c/\sqrt{n}\)) associado à média da amostra?
☞ sugestões
o que representa \(s_c\)? e n?
na tabela no enunciadono R, «sd» quer dizer «desvio padrão corrigido» (Standard Deviation);
basta aplicar a expressão aos dados no enunciado.
☞ solução
\(s_c/\sqrt{n} \approx 1.14673\);
(d) Através do QQ-plot averigue se pode considerar que os dados são provenientes de uma distribuição normal, validando os IC obtidos nas alíneas anteriores.
☞ sugestões
Consulte a interpretação de um QQplot normal;
☞ proposta de resolução
É de crer que os dados provêm duma população normal pois os pontos estão próximos do segmento de reta no gráfico QQplot.
☞ mostrar código R
#Primeira vez:
#install.packages("TeachingDemos")
dados = read.csv("https://sweet.ua.pt/pedrocruz/dados/arvores.csv", dec=".", sep=",")
alturas = dados$ALTURA
summary(alturas)
qqnorm(alturas, datax=TRUE, pch=20)
qqline(alturas, datax=TRUE, pch=20, lwd=2, col="red")
t.test(alturas)