testes de independência
Num teste de independência é avaliado se dois fatores são independentes ou correlacionados.
H0: há «independência» entre dois fatores
H1: há «associação» (ou «dependência») entre dois fatores
Nota: o procedimento é idêntico ao teste de homogeneidade.
independência
Quando A e B são independentes então \(P(A \cap B) = P(A) \times P(B)\). Esta propriedade resulta quando os acontecimentos A e B verificam
e \(P(A) \times P(B)>0\).
Em resumo, a ocorrência de um acontecimento não condiciona a probabilidade da ocorrência do outro. Para uma maior clarificação e detalhe consulte Martins, E.G.M., (2017) Acontecimentos independentes, Rev. Ciência Elem., V5(4):049
exemplo
Existe associação significativa entre a cor de uma flor de uma espécie de planta e a existência de um tipo de parasita?
Avaliaram-se 200 exemplares dessa espécie e registou-se a cor (amarela, rosa e vermelha) e a existência (sim ou não) do parasita.
O total por linha usa a notação \(n_{i\bullet}\):
\(n_{1\bullet}\) = «total da primeira linha» = 128
\(n_{2\bullet}\) = «total da segunda linha» = 45
\(n_{3\bullet}\) = «total da terceira linha» = 27
O total por coluna usa a notação \(n_{\bullet j}\):
\(n_{\bullet1}\) = «total da primeira coluna» = 68
\(n_{\bullet2}\) = «total da sgunda coluna» = 132
O total absoluto de observações é \(n=200\).
estatística de teste e pressupostos
em que
\(n_{ij}\) representa a frequência observada pelo investigador para a célula (i,j);
\(e_{ij}\) representa a frequência esperada assumindo que H0 é verdade (independência entre fatores);
r é o número de linhas (número de grupos do fator A);
c é o número de colunas (número de grupos do fator B).
Pressupostos: as seguintes regras ajudam a reduzir o erro da decisão. Se o número total de observações
é \(n \le 20\) então as frequências esperadas \(e_{ij}\) não devem ser inferiores a 5 unidades;
é \(n > 20\) então não devem existir mais de 20% de células com frequências esperadas \(e_{ij}\) inferiores a 5 unidades e nenhuma célula deve ter frequência esperada inferior a 1.
procedimento
- 1. Identificar as duas categorias e seus níveis.
A categoria, ou fator, divide-se em níveis, tratamentos ou grupos.
No exemplo, a categoria «cor» divide a amostra de flores em: «amarelas, «rosa» e «vermelha». A categoria «parasita», dividide a amostra em «sim» e «não.
- 2. Definir as hipóteses
A independencia entre os fatores é testada:
H0: a «cor» e a «existência de parasita» são fatores independentes.
H1: a «cor» e a «existência de parasita» são fatores dependentes.
- 3. Calcular os valores esperados caso H0 seja verdade.
Os valores esperados, na estatśitica do qui-quadrado de Pearson, são dados por
Assim, para o exemplo dado,
\(e_{11} = \frac{ n_{1 \bullet} \times n_{\bullet 1} }{n} = \frac{128 \times 68}{200}=42.52\)
\(e_{12} = \frac{ n_{1 \bullet} \times n_{\bullet 2} }{n} = \frac{128 \times 132}{200}=84.48\)
\(e_{21} = \frac{ n_{2 \bullet} \times n_{\bullet 1} }{n} = \frac{45 \times 68}{200}=15.3\)
\(e_{22} = \frac{ n_{2 \bullet} \times n_{\bullet 2} }{n} = \frac{45 \times 132}{200}=28.7\)
\(e_{31} = \frac{ n_{3 \bullet} \times n_{\bullet 1} }{n} = \frac{27 \times 68}{200}=9.18\)
\(e_{32} = \frac{ n_{3 \bullet} \times n_{\bullet 2} }{n} = \frac{27 \times 132}{200}=17.82\)
- 3. Calcular o valor observado da estatística de teste.
Usando o teste do qui-quadrado de Pearson:
A tabela do exemplo tem 6 células sendo \(r=3\) (rows) e \(c=2\) (columns). O somatório terá 6 parcelas:
\[\chi^2_{obs} = \frac{ (n_{11} - e_{11})^2 }{ e_{11} } + \cdots + \frac{ (n_{32} - e_{32})^2 }{ e_{32} }\]
Recorda-se a tabela de observações \(n_{ij}\):
sim |
não |
|
amarela |
50 |
78 |
rosa |
10 |
35 |
vermelha |
8 |
19 |
sendo a soma das parcelas dada por
\(\displaystyle\frac{(50 - 42.52)^2}{42.52}\) |
\(\displaystyle\frac{(78 - 84.48)^2}{84.48}\) |
\(\displaystyle\frac{(10 - 15.3 )^2}{15.3}\) |
\(\displaystyle\frac{(35 - 29.7 )^2}{29.7}\) |
\(\displaystyle\frac{( 8 - 9.18)^2}{9.18}\) |
\(\displaystyle\frac{(19 - 17.82)^2}{17-82}\) |
Os graus de liberdade são dados por:
O seguinte esboço gráfico marca o valor-p (depois de 4.82446) para a distribuição qui-quadrado com 2 graus de liberdade:
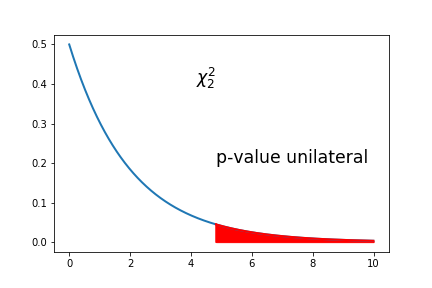
- 4. Calcular o valor observado da estatística de teste.
Usando o teste do qui-quadrado de Pearson:
valor-p unilateral direito = CDF.chisq(lower=4.82446, upper=+infinito, df=2) = 0.08961523
- 5. Conclusão.
Considerando-se os níveis usuais de significância:
\(\alpha=1\%\) então não se rejeita a hipótese de independência entre os fatores cor e existência de parasita;
\(\alpha=5\%\) então não se rejeita a hipótese de independência entre os fatores cor e existência de parasita;
\(\alpha=10\%\) então rejeita-se a hipótese de independência entre os fatores cor e existência de parasita.
Comentário: o resultado do teste é aproximado devido à estatística de teste ter, apenas de forma aproximada via TLC, a distribuição do qui-quadrado. Como neste exemplo há uma dupla decisão consoante o \(\alpha\) recomenda-se aumentar a amostra a fim de melhorar a segurança da decisão.
- 6. Pressupostos.
Esta etapa ajuda a reduzir o erro da decisão.
Recordando, se o número total de observações é
\(n \le 20\) então as frequências esperadas \(e_{ij}\) não devem ser inferiores a 5 unidades;
\(n > 20\) então não devem existir mais de 20% de células com frequências esperadas \(e_{ij}\) inferiores a 5 unidades e nenhuma célula deve ter frequência esperada inferior a 1.
No exemplo, \(n=200\) e \(e_{ij} > 5\), e deste modo os pressupostos que minoram uma tomada de decisão errada devido à aproximação da distribuição estão verificados.