ex. 4.10

Recolheram-se 5 amostras de fitoplancton (milhares de unidades por litro) em dois locais de um lago durante o mês de Maio. O procedimento foi repetido em Agosto.

Os dados na tabela estão no ficheiro fitoplanton.csv.

Local I	Maio	108	113	119	109	112
	Agosto	97	103	109	98	102
Local II	Maio	111	116	120	111	113
	Agosto	106	110	116	105	111

Tendo em conta o seguinte resultado do R, considerando os pressupostos de uma ANOVA paramétrica apropriada, teste a existência de diferenças significativas entre locais, períodos de recolha e a interação entre local e tempo. Use o nível de significância 5%.

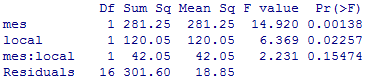
☞ sugestões

De que tipo de ANOVA se trata?

• ANOVA a 1 fator de efeitos fixos ?

• ANOVA a 1 fator de efeitos aleatórios?

• ANOVA a 2 fatores de efeitos fixos?

• ANOVA de Medidas Repetidas?

A tabela pode ser escrita assim:

	Maio	Agosto
Local 1	108	97
	113	103
	119	109
	109	98
	112	102
Local 2	111	106
	116	110
	120	116
	111	105
	113	111

• Assim, trata-se de uma ANOVA factorial com dois fatores fixos.

☞ solução

Fator mês: «maio» e «agosto»

• mês é o fator

• «maio» e «agosto» são os níveis (ou tratamentos ou grupos)

Fator local: «local 1» e «local 2»

• local é o fator

• «local 1» e «local 2» são os níveis (ou tratamentos ou grupos)

Y = fictoplanton (milhares de unidades por litro)

Teste de hipóteses ao fator Mês:

• $H_0: \mu_{maio}=\mu_{agosto}$ vs $H_0: \mu_{maio} \neq \mu_{agosto}$

• p-value(Fator Mês) = 0.001 (rejeitar H0 pois p-value < 5%)

• Mês: a média de fitoplancton varia significativamente com o mês.

Teste de hipóteses ao fator Local:

• $H_0: \mu_{local 1}=\mu_{local 2}$ vs $H_0: \mu_{local 1}\neq\mu_{local 2}$

• p-value (Fator Local) = 0.02 (rejeitar H0 pois p-value < 5%)

• Local: a média de fitoplancton varia significativamente com o Local.

Teste de hipóteses à interação:

• p-value (interação) = 0.15 (não rejeitar H0 pois > 5%)

• Não há interação entre o fator mês e o fator local.

• H0: não há interação

• H1: há interação