ex. 4.4
Com o intuito de estudar a influência da temperatura ambiente na capacidade de trabalho das pessoas, 80 estudantes universitários foram divididos em 4 grupos equilibrados que foram sujeitos a 4 temperaturas seleccionadas ao acaso. Cada aluno teve de responder a um conjunto de 150 questões simples tendo sido contabilizado o número de respostas correctas. Os dados obtidos encontram-se no ficheiro respostas.csv.
Com esse conjunto de dados foram construídos os gráficos e tabelas que se seguem:
(a) Comente as seguintes caixas de bigodes comparativas.
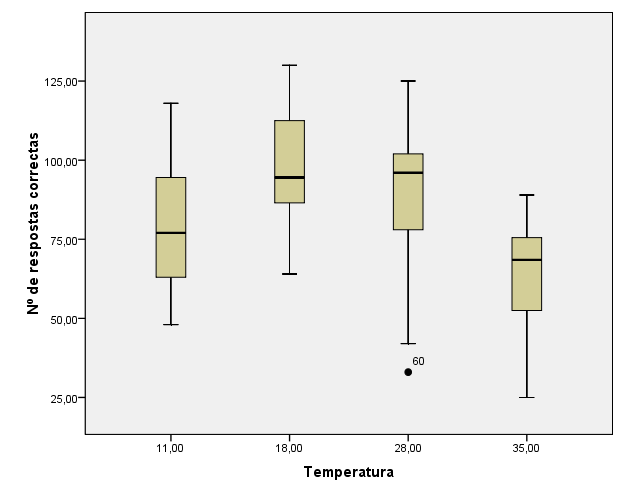
☞ sugestões
☞ solução
O gráfico sugere que a temperatura influencia a capacidade de trabalho; particularmente as temperaturas intermédias (as duas do meio), parecem sugerir maior capacidade de trabalho.
(b) Comente os gráficos de quantis dos diferentes grupos, avalie a possibilidade de efectuar uma ANOVA paramétrica.
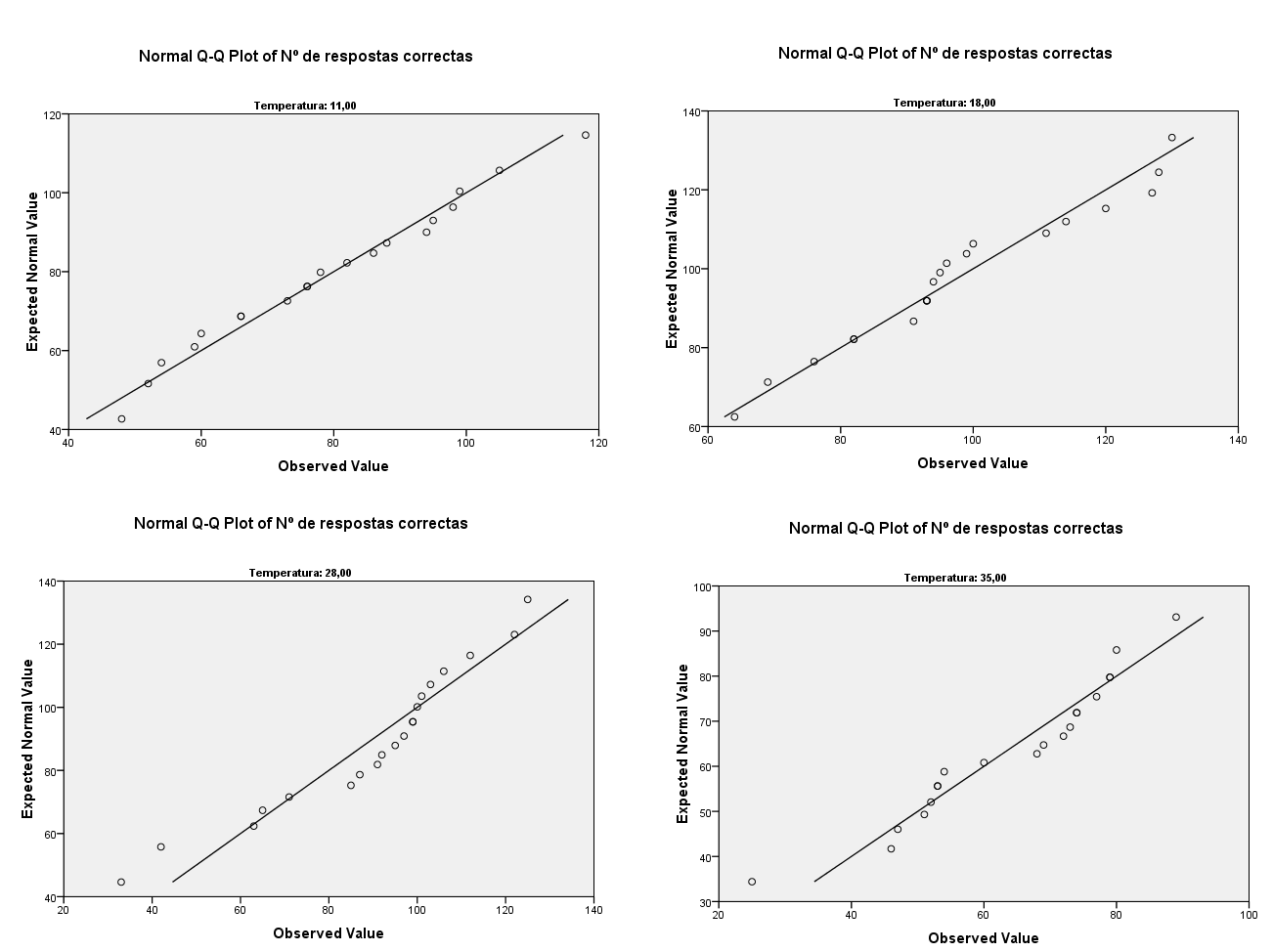
☞ sugestões
Consulte os pressupostos (conceitos) de uma ANOVA paramétrica.
☞ solução
Não parece haver motivo para rejeitar a normalidade das observações em cada um dos grupos, devido à proximidade dos pontos relativamente às rectas.
Não se dispõe de informação acerca da homogeneidade de variâncias que é outro pressuposto que deve ser verificado.
(c) Foi realizada uma ANOVA de efeitos aleatórios. Com recurso ao R obteve-se: (\(\alpha=0.05\))

Com base na informação dada responda às sub-alíneas:
☞ sugestões
(c-i) Escreva as hipóteses em teste.
☞ solução
A resposta precisa é:
\(H_0: \sigma_\tau^2=0\) vs \(H_1: \sigma_\tau^2 \neq 0\)
que diz que se a variância :math:` sigma_tau^2`, de \(\tau_i\), não é significativa então \(\tau_i \approx 0.0\) e as médias de cada grupo não serão significativamente diferentes:
\(H_0: \mu_1 = \mu_2 = \cdots = \mu_k\)
pois \(Y_{ij} = \mu + \tau_i \approx \mu\).
(c-ii) Registe o valor da estatística de teste.
☞ sugestões
A estatística de teste, \(F_{obs}\), está no coração da:
☞ solução
\($F_{obs} = \frac{MS_G}{MS_E} = \frac{4331}{388} = 11.17\)
(c-iii) Registe o valor-p do teste.
☞ sugestões
p-value=CDF.F( 11.17, +infinito, df1=3, df2=76)
☞ solução
p-value=:math:3.7x10^{-6} approx 0.0
(c-iv) Tome a decisão do teste e conclua no contexto do problema.
☞ solução
Como \(p<0.05\), rejeita-se \(H_0\), i.e., conclui-se que a temperatura ambiente influi significativamente na capacidade de trabalho, em média (tal como era sugerido pelo gráfico da caixa-de-bigodes)
Outras frases análogas:
existe pelo menos uma performance média, de uma sala a uma da temperatura, que é significativamente diferente das outras
a variabilidade média causada pela escolha da temperatura é significativa.
(d) No caso de concluir que a temperatura influencia a capacidade de trabalho, forneça uma estimativa da variância, :math:´sigma_{tau}^2`.
☞ sugestões
Os conceitos são:
\(\tau_i \sim N(0, \sigma^2_\tau)\);
\(\tau_i\) são desvios face à média comum (no caso de «efeitos aleatórios», \(\tau_i\) é uma v.a.);
o teste já indicou que a variância \(\sigma^2_\tau\) é significativa, i.e., há influência significativa da temperatura.
☞ solução
\(\hat{\sigma}_\tau^2=\frac{MS_G-MS_E}{n}= \frac{4331 - 388}{20} = 197.1384\)
Nota: \(MS_G\) é «mean square of groups» e \(MQ_G\) é «média de quadrados dos grupos».