ex. 4.2 (*)
A anemia é uma doença que afecta muitas pessoas e que pode ter diversas origens. Pretendendo-se avaliar possíveis diferenças entre diferentes tratamentos de estados anémicos, planeou-se uma experiência com 120 indivíduos anémicos, divididos aleatoriamente em três grupos de 40, aos quais se atribuiu cada um dos tratamentos. O primeiro tratamento era constituído apenas por uma dieta rica em ferro. O segundo tratamento combinava um suplemento de ferro com a dieta do primeiro tratamento e o último acrescentava um complexo vitamínico. No sentido de avaliar possíveis diferenças entre os tratamentos, efectuou-se uma ANOVA com base nos valores de hemoglobina dos 120 indivíduos após um período de 3 meses de tratamento. Os resultados da ANOVA encontram-se na tabela seguinte. Complete a tabela nos espaços apropriados.
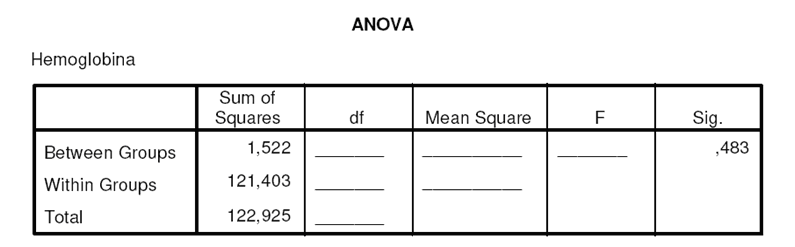
☞ sugestões
☞ proposta de resolução
Da frase
«planeou-se uma experiência com 120 indivíduos anémicos, divididos aleatoriamente em três grupos de 40, aos quais se atribuiu cada um dos tratamentos.»
entende-se que
o fator é o tipo de tratamento contra a anemia
a medição do efeito do tratamento foi em N = 120 indivíduos (independentes); N é a totalidade de observações
estes foram divididos, num planeamento equilibrado em 3 tratamentos (g=3, também se usa k=3); pode ainda usar-se 3 grupos ou 3 níveis
Em resumo: N=120 e g=3 (no slides k=3)
A frase:
«O primeiro tratamento era constituído apenas por uma dieta rica em ferro. O segundo tratamento combinava um suplemento de ferro com a dieta do primeiro tratamento e o último acrescentava um complexo vitamínico.»
confirma os g=3 (ou k=3, como nos slides) tratamentos e descreve-os.
Há dois tipos de variância, ou variabilidade, que na ANOVA se chama de «média de quadrados». Os seguintes passos ilustram a formas de variabilidade devida ao tratamento (ou devida ao grupo):
se um tratamentos tiver um «grande efeito» então a média das observações, devidas a esse tratamento, será significativamente diferentes das médias dos outros tratamentos;
no enunciado, existem três médias porque há três tratamentos (g=3, ou k=3);
existindo três média, e sendo pelo menos uma significativamente diferente, então há variabilidade
tal causa que a soma dos quadrados \((\bar y_i - \bar y)^2\) seja elevada (em relação aos erros)
O que são os erros?
Dentro de cada tratamento (ou grupo) há medições em torno de uma média.
Esses desvios à média do grupo, chamam-se de erros (ou resíduos quando se menciona um valor concreto).
Se a variabilidade observada só nos três tratamento médios (grupos) é significativamente mais elevada que a variabilidade média dos pequenos erros às médias de cada grupo então existe pelo menos um tratamento significativamente diferente, em média.
Em termos de quantidades:
a variabilidade devida aos tratamentos (grupos) chama-se «média de quadrados dos grupos» (MSG)
a variabilidade devida aos erros chama-se «média de quadrados dos erros» (MSE)
o teste F (o mesmo da comparação de duas populações indepedentes) volta a ser necessário para comparar estas duas «variâncias», chamadas de «MSG» e «MSE»;
e o valor-p é abaixo de alfa então rejeita-se a igualdade das médias existindo pelo menos uma média populacional diferente das outras.
Os cálculos são:
df (graus de liberdade) dos grupos: g-1 (ou k-1 nos slides)
df dos erros: N-g ( ou N-k nos slides)
SSG é a soma de quadrados dos grupos
SSE é a soma de quadrados dos erros
MSG = SSG/(g-1), (k nos slides)
MSE = SSE/(N-g), (k nos slides)
F observado na grande amostra: F=MSG/MSE
valor-p = CDF.F(F, g-1, N-g)
\(g-1=2\), \(g(n-1)=117\), \(ng-1=119\), \(MS_G=0.761\), \(MS_E=1.038\); \(F_{obs}=0.733\)