ex. 4.1
Um biólogo está interessado em estudar 3 variedades diferentes de trigo. O objectivo é averiguar se o tamanho médio dos grãos se pode considerar igual para as três variedades. Para tal foram seleccionados 12 campos considerados homogéneos (mesmo tipo de solo e de condiçõeses climáticas) que foram divididos em trêss grupos de 4, de forma aleatória.
As 3 variedades foram atribuídas aleatoriamente a cada um dos grupos de campos e ao fim de 3 meses decrescimento foi feita uma colheita de grãos de cada campo e calculado o peso médio do hectolitro de cada colheita.
Os resultados foram:
variedade 1 |
variedade 2 |
variedade 3 |
|---|---|---|
78 |
75 |
70 |
79 |
74 |
71 |
76 |
76 |
69 |
75 |
73 |
70 |
(a) Assuma que os pressupostos da ANOVA paramétrica são válidos e, com recurso à calculadora, complete a seguinte tabela:
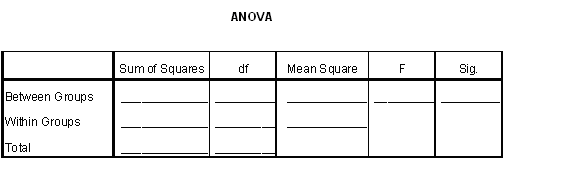
☞ sugestões
Sig é o valor-p;
df: degrees of freedom, graus de liberdade;
Within Groups quer dizer «variância dentro dos grupos» (ou variância dos resíduos/erros).
☞ solução
Sum of Squares |
df |
Mean Square |
\(F_{obs}\) |
valor-p |
|
Between Groups |
\(SS_G=100.667\) |
\(g-1=2\) |
\(MS_G=50.333\) |
\(26.647\) |
\(0.0\) |
Within Groups |
\(SS_E=17.0\) |
\(g(n-1)=9\) |
\(MS_E=1.889\) |
||
Total |
\(SS_T=117.667\) |
\(ng-1=11\) |