ex. 5.15
Foi efetuada uma análise de regressão linear relacionando variáveis x, a variável independente, e Y|x, a variável que dependende de x.
Os resultados estão nas seguintes tabelas:
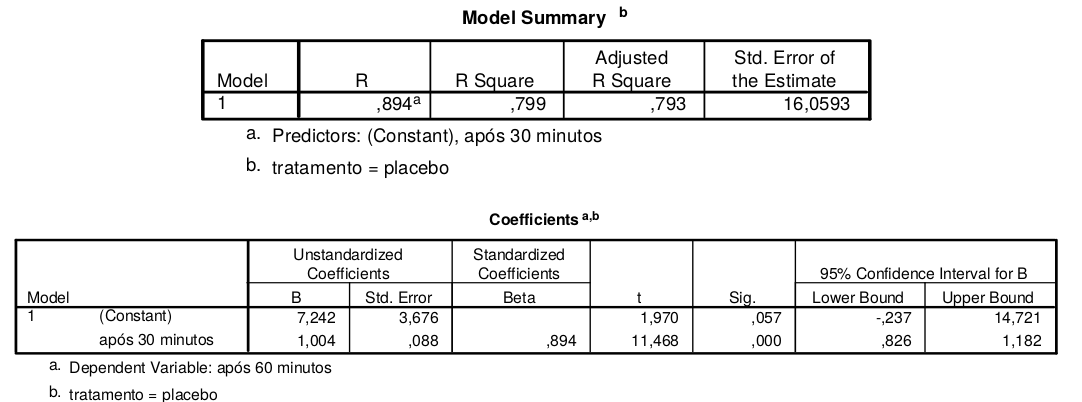
(a) Qual a equação da reta de regressão?
☞ solução
y=7.242 + 1.004 x
As estimativas (e sua notação) são: \(\hat \beta_0=7.242\) e \(\hat \beta_1=1.004\) (há um erro no pdf-papel)
(b) Teste se a ordenada na origem é significativamente diferente de zero, fixando \(\alpha = 0.05\) sabendo que são n=36 pontos na amostra. Na sua resposta:
Escreva as hipóteses em causa: H0 vs H1.
Qual o valor observado da estatística de teste?
Qual o p-value do teste?
O que conclui?
☞ solução
A notação usual diz que \(\beta_0\) é a ordenada na origem.
O valor da estatística de teste \(t_{obs}\) do coeficiente \(\beta_0\) é obtido na coluna «t»: 1.970 e corresponde a \(\hat \beta_0 / \hat \sigma_0\).
O p-value é 0.057; assim, não se rejeita a hipótese de ordenada na origem ser nula, isto é, considera-se a possibilidade da reta regressão ter a forma \(y=\beta_1 x\).
(c) Utilizando o Intervalo de Confiança fornecido na tabela, teste se o declive é significativamente diferente de 1.
☞ solução
Não se rejeita \(H_0:\beta_1=1\) pois \(\beta_1=1 \in [0.026,\;1.182]\).
O grau de confiança do IC é 95% e o teste de hipóteses está a ser pedido com nível de significância de 5% (só pode ser 5%).
(d) Qual o valor do coeficiente de determinação? O que significa esse valor.
☞ solução
\(R^2=0.799\).
Aproximadamente 80% da variação em Y depende linearmente da variação em x. os restantes 20% da variabilidade de Y deve-se a erros da observação face ao modelo da reta.