ex. 5.14

Numa análise de regressão foi efetuada a seguinte análise dos resíduos ($e_i = y_i - \hat y_i$, i=1,…,36).

Com base nos testes de ajustamento à normalidade responda às questões seguintes.

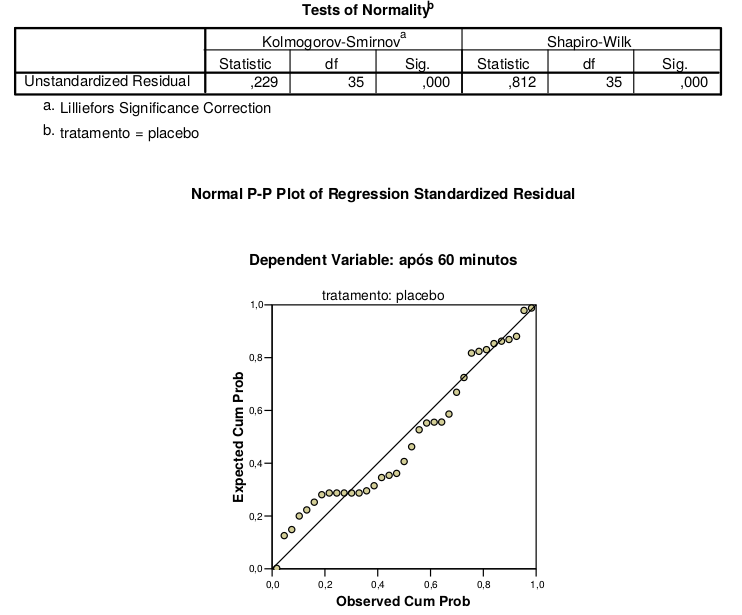
(a) Indique o que significa $y_i$, $\hat y_i$ e $e_i$?

☞ solução

• $y_i$ é o valor de resposta observado para um dado $x_i$ em que a medida observada $y_i$ contém um erro (na regressão são registados pares $(x_i,y_i)$;

• $\hat y_i=$ é um valor que pertence à reta de regressão para um dado $x_i$ resultante da equação $\hat y_i = \beta_0 + \beta_1 x_i$ (portanto, sem o erro);

• $e_i$ é o resíduo (uma concretização da v.a. do erro $\epsilon$), isto é, a diferença entre o valor observado na amostra $y_i$ e o valor predito na reta de regressão $\hat y_i = \beta_0 + \beta_1 x_i$.

(b) Que conclusão tira da análise de resíduos?

☞ solução

Ambos rejeitam a normalidade dos erros, isto é, perante as hipóteses:

$$H_0:\, \epsilon \sim \text{Normal} \text{ vs } H_1:\, \epsilon \not \sim \text{Normal}$$

rejeita-se $H_0$. Assim, o pressuposto de regressão linear paramétrica é rejeitado; não faz sentido aplicar regressão linear com este preciso modelo:

$$Y = \beta_0 + \beta_1 x + \epsilon, \quad \epsilon \sim N(0,\sigma^2)$$