ex. 4.16 (*)
Um biólogo pretende verificar o efeito de um pesticida sobre as larvas de um mosquito. Para o efeito, foram tratadas com pesticida algumas áreas agrícolas e, posteriormente, contabilizado o número de larvas existentes em charcos de áreas tratadas e não tratadas. O conjunto de dados recolhidos corresponde ao número de larvas por charco, divididos por 100, e medidas dos dados estão sumariados na seguinte tabela:
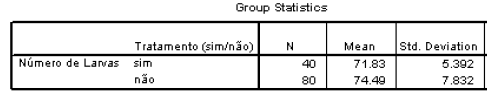
(a) Quais os pressupostos inerentes à realização de um teste t para comparação de médias?
☞ sugestões
(por fazer)
☞ proposta de resolução
Ambas as populações devem ser normais e o desvio populacional não deve ser conhecido (caso contrário, usa-se o teste Z).
(b) Valide os pressupostos de normalidade com os seguintes QQ-Plots.
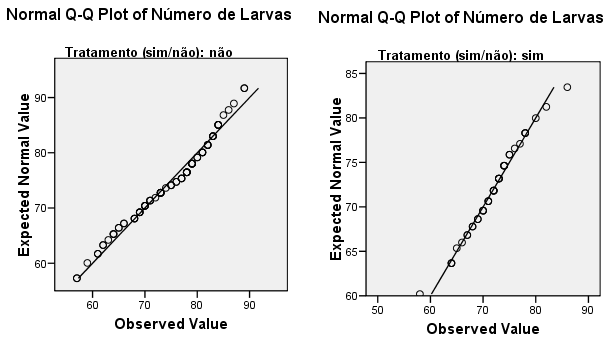
☞ sugestões
(por fazer)
☞ solução
Os QQ-Plots apresentados mostram bom ajustamento das amostras à distribuição normal.
(c) Com base nos dados observados, efetue um teste t para averiguar se o número médio de larvas é significativamente diferente nas áreas tratadas e não tratadas (\(\alpha = 0.01\)).
(i) Escreva as hipóteses.
☞ sugestões
(por fazer)
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
\(H_0\, :\,\mu_X=\mu_Y$ vs $H_1\,:\,\mu_X \neq \mu_Y\), onde X é o número de larvas em áreas não tratadas e Y é o número de larvas em áreas tratadas.
(Resolução usando o SPSS (que usa o teste de Levene)):
- \(H_0\, :\,\mu_X=\mu_Y$ vs $H_1\,:\,\mu_X \neq \mu_Y\), onde X é o
número de larvas em áreas não tratadas e Y é o número de larvas em áreas tratadas.
(ii) O que pode dizer sobre a homogeneidade das variâncias?
☞ sugestões
(por fazer)
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
Não se rejeita a homogeneidade das variâncias, pois o valor-p do teste F é 0.011, logo é superior ao nível de significância exigido (\(\alpha=1\%\)) e, neste caso, na máquina, deve escolher-se pooled=ON).
(Resolução usando o SPSS (que usa o teste de Levene)):
Rejeita-se a homogeneidade das variâncias, pois o valor-p do teste de Levene é muito baixo.
(iii) Registe o valor-p do teste t.
☞ sugestões
A reflectir:
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
O valor-p do teste bilateral é 0.056 (5.6%).
(Resolução usando o SPSS (que usa o teste de Levene)):
O valor-p do teste bilateral é 0.032.
(iv) Conclua.
☞ sugestões
A reflectir.
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
Sendo o valor-p superior a \(\alpha=0.01\), não temos razões para rejeitar a igualdade das médias \(\mu_X\) e \(\mu_Y\).
(Resolução usando o SPSS (que usa o teste de Levene)):
Sendo \(\alpha=0.01\) um valor abaixo do valor-p, não temos razões para rejeitar a igualdade das médias \(\mu_X\) e \(\mu_Y\).
(d) Efetue um teste t para averiguar se o número médio de larvas é significativamente inferior nas áreas tratadas relativamente às não tratadas (\(\alpha = 0.01\)).
(i) Escreva as hipóteses.
☞ sugestões
A reflectir:
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
\(H_0\, :\,\mu_X=\mu_Y$ vs $H_1\,:\,\mu_X > \mu_Y\).
(Resolução usando o SPSS (que usa o teste de Levene)):
\(H_0\, :\,\mu_X=\mu_Y$ vs $H_1\,:\,\mu_X > \mu_Y\).
(ii) Determine o valor-p do teste t (unilateral).
☞ sugestões
A reflectir
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
Como \(t_{obs}=2.179\) aponta no sentido de \(H_1\), então o valor-p unilateral (à direita) é \(0.056/2=0.028\).
(Resolução usando o SPSS (que usa o teste de Levene)):
Como \(t_{obs}=2.179\) aponta no sentido de \(H_1\), então o valor-p unilateral (à direita) é \(0.032/2=0.016\).
(iii) Conclua.
☞ sugestões
(por fazer)
☞ proposta de resolução
(Resolução usando a calculadora (e teste F para variâncias)):
O valor-p unilateral (à direita) \(0.056/2=0.028\) é superior ao valor \(\alpha=0.01\) e, assim, não se rejeita \(H_0\).
(Resolução usando o SPSS (que usa o teste de Levene)):
O valor-p unilateral (à direita) é \(0.032/2=0.016\) é superior ao valor \(\alpha\) e assim não se rejeita \(H_0\).