ex. 4.14 (*)
Um biólogo pretende verificar o efeito de um pesticida sobre as larvas de um mosquito. Para o efeito, foram tratadas com pesticida algumas áreas agrícolas e, posteriormente, contabilizado o número de larvas existentes em charcos de áreas tratadas e não tratadas (e dividido, cada número, por 100).
Assuma a normalidade dos dados.
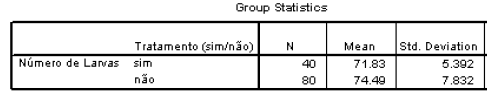
Encontre um intervalo de confiança para a diferença de médias do número de larvas das populações tratadas e não tratadas, com um grau de confiança de 95%, com base nos seguintes resultados registados para o conjunto dos 120 charcos analisados:
☞ sugestões
☞ solução
Rejeita-se a igualdade de variâncias (valor \(p<0.05\))
\((-5.085,-0.240)\)
☞ proposta de resolução
Tratam-se de amostras independentes porque as áreas são independentes: umas para tratamento com pesticida e outras sem tratamento. (Nota: não poderiam ser emparelhadas porque as áreas tratadas foram 40 e a não tratadas foram 80.)
A ordem das variáveis deve seguir a ordem na tabela no enunciado:
X = número de larvas numa área agrícola tratada Y = número de larvas numa área agrícola não tratada
Da frase «Assuma a normalidade dos dados» tiramos que
\(X \sim Normal(\mu_X, \sigma_X^2)\)
\(Y \sim Normal(\mu_Y, \sigma^2_Y)\)
em que os 4 parâmetros são desconhecidos.
O enunciado pede um intervalo de confiança para as médias mas o que deve ser feito em primeiro é o teste F de homogeneidade («igualdade») das duas variâncias, como se descreve.
Como as variâncias populacionais não são conhecidas é necessário, primeiro, testar a homogeneidade das variâncias:
H0: \(\frac{\sigma_X^2}{\sigma_Y^2}=1\) ou \(\sigma_X^2 = \sigma_Y^2}\) vs. H1: \(\frac{\sigma_X^2}{\sigma_Y^2} \neq 1\) ou \(\sigma_X^2 \neq \sigma_Y^2\)
De seguida, realiza-se o teste F de Fisher «à mão» (mas pode ser feito com a calculadora). Esse teste usa a estatística de teste:
em que n-1=39 e m-1=79 de acordo com os dados na tabela.
A distribuição F não é simétrica e tem as medidas de centralidade em torno de 1, especialmente com amostras já grandes. Assim, o valor 0.4739739 sendo «bastante» inferior a 1 calcula-se o valor-p bilateral com a expressão:
com calculadora ou sistema R:
> pf(0.4739739, 39,79) * 2
[1] 0.01164028
Assim, ao nível de significância de 5% rejeita-se a homogeneidadede variâncias (rejeita-se H0: \(\frac{\sigma_X^2}{\sigma_Y^2}=1\))
O intervalo de confiança para \(\mu_X - \mu_Y\) deve ser feito com «Pooled=Off» nas calculadoras.
Resposta: \([-5.0853715 -0.2396285]\)
Apresenta-se uma resolução com recurso ao r dada a complexidade das fórmulas no caso de variâncias não homogéneas. Estes comandos partem das amostras independentes e não apenas das suas médias e desvios padrão amostrais.
# Leitura de dados:
> dados <- read.csv("https://sweet.ua.pt/pedrocruz/dados/larvas.csv", sep=",", fileEncoding="utf8")
> X = dados[dados$tratada=="sim", ]$numlarvas
> Y = dados[dados$tratada=="não", ]$numlarvas
> var.test(X,y)
F test to compare two variances
data: X,Y
F = 0.47392, num df = 39, denom df = 79, p-value = 0.01163
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.2808665 0.8419446
sample estimates:
ratio of variances
0.4739222
# teste t com "pooled=FALSE"
> t.test(X, Y, var.equal=FALSE)
Welch Two Sample t-test
data: X, Y
t = -2.1786, df = 106.29, p-value = 0.03157
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-5.0853715 -0.2396285
sample estimates:
mean of x mean of y
71.8250 74.4875
Resposta: \([-5.0853715 -0.2396285]\)