ex. 3.16

O ficheiro camaroes.csv contém uma amostra de valores correspondentes ao comprimento dos corpos de 60 camarões de aquacultura selecionados aleatoriamente. A média da amostra é 5.315 e o respetivo desvio padrão corrigido é 0.8293.

(a) Efetue um teste t, através do cálculo da região crítica, para averiguar se a média é significativamente diferente de 5.15 ($\alpha = 0.05$).

☞ sugestões

Consulte o método em TH com base na região crítica.

☞ solução

$H_0:\,\mu=5.15$ vs $H_1:\,\mu\neq 5.15$;

$t_{obs}=1.54$; valor-p = 0.128; Não há razões para rejeitar $H_0$, i.e., o comprimento esperado do corpo de um camarão não é significativamente diferente de 5.15;

(b) Efetue um teste t para averiguar se a média é significativamente superior a 5.15 ($\alpha = 0.1$).

☞ sugestões

Sugere-se o método do p-value:

consulte TH com base no p-value.

☞ solução

$H_0\,:\,\mu=5.15$ vs $H_1\,:\,\mu > 5.15$;

$t_{obs}=1.54$;

Há razões para rejeitar $H_0$ pois valor-p unilateral à direita é 0.06431.

O comprimento esperado do corpo de um camarão é significativamente superior a 5.15.

(c) Com base no seguinte QQ-plot associado aos dados, o que pode dizer sobre o pressuposto de normalidade inerentes à realização de um teste t sobre a média populacional?

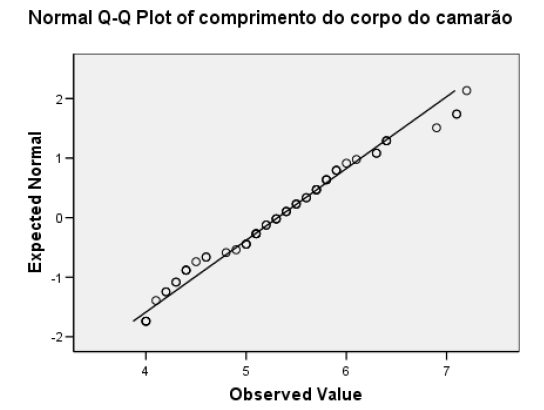
☞ sugestões

Consultas úteis:

☞ solução

O QQPlot não invalida a hipótese de normalidade do comprimento dos camarões ($X$) sendo esta uma condição necessária para usarmos o teste t.