ex. 2.25 (*)

Num determinado genoma, a probabilidade de num conter o alelo recessivo «a» é 0.3 e a probabilidade de ocorrência do alelo dominante «A» é 0.7. Considere a presença conjunta destes alelos é independente.

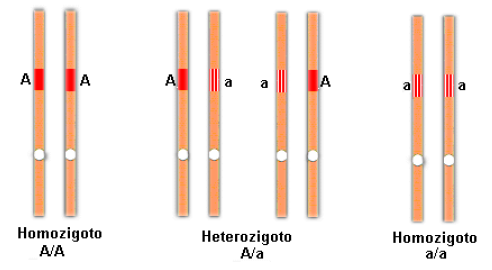
Calcule a probabilidade de encontrar os diferentes genótipos “AA”, “Aa” e “aa”.

_images/d-empirica-alelos.png

☞ proposta de resolução

Quando duas ocorrências, A e B, são independentes então verifica-se a seguinte propriedade das probabilidades:

\[P(A \cap B) = P(A) \times P(B) \quad\text{se A e B são ocorrências independentes}.\]

Ou seja, o surgimento de um tipo de alelo, neste exercício, não causa o surgimento do outro tipo de alelo.

Assim, assumindo que a associação entre alelos é independente então a probabilidade de encontrar o par é a multiplicação das probabilidades de encontrar cada alelo individualmente:

  • Caso homozigoto AA: 0.7 x 0.7 = 0.49

  • Caso Heterozigoto Aa: 0.7 x 0.3 = 0.21

  • Caso Heterozigoto aA: 0.3 x 0.7 = 0.21

  • Caso homozigoto aa: 0.3 x 0.3 = 0.09

Assim,

  • Caso AA: 0.7 * 0.7 = 0.49

  • Caso Aa: 0.7 * 0.3 + 0.3 * 0.7 = 0.42

  • Caso aa: 0.3 * 0.3 = 0.09