ex. 1.10 (*)

Num estudo sobre o número de golfinhos presos diariamente em redes de pesca ao largo dos Açores, nos 257 dias de 1998 em que o estado do tempo permitiu a saída de barcos, obtiveram-se os dados que se seguem:

Nº de golfinhos	0	1	2	3	4	5	6	8	9	13
Nº de dias	37	45	84	52	23	11	2	1	1	1

(a) Diga qual a variável em estudo e classifique-a (tipo e escala de medida).

☞ solução

• variável: «Número de golfinhos presos por dia em redes de pesca ao largo dos Açores»;

• tipo e escala: quantitativa discreta, escala de razões.

(b) Encontre a mediana e o percentil de ordem 30 e interprete os valores obtidos (primeiro sem usar a calculadora e depois, comparando os resultados com os da calculadora).

☞ solução

• Mediana=2, ($m_e=2$ ou $x_{0.5}=2$). Veja como calcular a mediana em dados agrupados aqui.

Interpretação: em pelo menos 50% dos dias em que o estado do tempo permitiu a saída de barcos, foram encontrados até 2 golfinhos presos nas redes. Para a resposta ficar correta em termos de rigor matemático, ainda é preciso indicar que em pelo menos 50% dias foram encontrados pelo menos 2 golfinhos presos nas redes.

• Percentil 30 é igual a 1, ($P_{30}=1$ ou $x_{0.3}=1$).

Interpretação: em pelo menos 30% dos dias em que o estado do tempo permitiu a saída de barcos, foram encontrados até 1 golfinhos presos nas redes e em pelo menos 70% dias foram encontrados pelo menos 1 golfinhos presos nas redes).

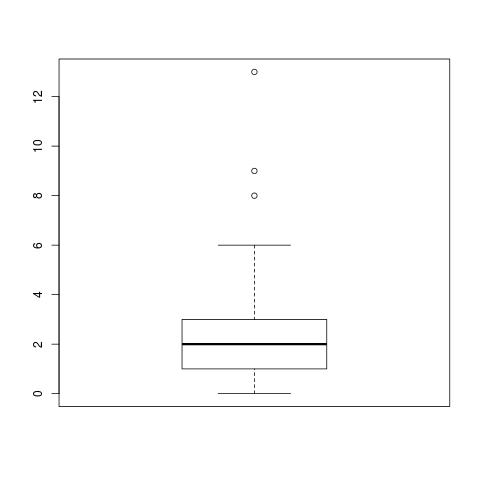
(c) Construa uma caixa de bigodes e descreva o conjunto de dados no que respeita à assimetria (primeiro sem usar a calculadora e depois, comparando os resultados com os da calculadora).

☞ solução

• Assimetria positiva:

  • de 0 a 2 ocorrem 50% das observações. Há por isso maior concentração em valores baixos e maior dispersão nos restantes valores.

• O boxplot seguinte foi feito em R que não implementa valores atípicos severos. A marca em 13 deve ser um «*».