ex. 6.4 (*)

No sentido de avaliar o equilíbrio Hardy-Weinberg, foi recolhida uma amostra aleatória de 100 descendentes.

Os resultados estão na tabela seguinte:

Genótipo	Frequência observada
$AA$	26
$Aa$	44
$aa$	30

Avalie se o modelo genético $(1/4\;:\;1/2\;:\;1/4)$ é adequado para essa população, fazendo o teste com e sem calculadora.

☞ sugestões

• Ver teste de ajustamento de Pearson.

• A notação $(1/4\;:\;1/2\;:\;1/4)$ indica as probabilidades esperadas de cada genótipo.

☞ proposta de resolução

As hipóteses são

• H0: a distribuição do genótipo na geração descendente é 1/4, 1/2 e 1/4;

• H1: a distribuição é outra.

A estatística de teste e a distribuição de amostragem são dadas por:

$$\chi^2 = \sum_{i=1}^k \frac{(n_i - n p_i)^2}{n p_i} \sim_{aprox} \chi^2_{k - p- 1}$$

onde k=3 classes e não existindo parâmetros a estimar então p=0. Assim, a distribuição é caracterizada por df = 2 graus de liberdade.

As probabilidades esperadas das classes são, de acordo com o enunciado,

• $(1/4 \;:\; 1/2\;:\;1/4)$

e sendo $n= 100$ o total de observações, então as frequências esperadas, caso H0 se verifique, são:

• $e_1=n \times 1/4=25$;

• $e_2=n \times 1/2=50$;

• $e_3=n \times 1/2=25$.

A tabela resume os valores:

Genótipo	Frequência observada	Frequência esperada
$AA$	26	25
$Aa$	44	50
$aa$	30	25

O valor observado da estatística de teste é

$$\begin{split}\begin{eqnarray*} \chi^2_{obs} & = & \frac{ (26-25)^2}{25} + \frac{(44-50)^2}{50} + \\ & & +\frac{(30-25)^2}{25} \\ & = & 1.76 \end{eqnarray*}\end{split}$$

Usando a notação CDF, tem-se:

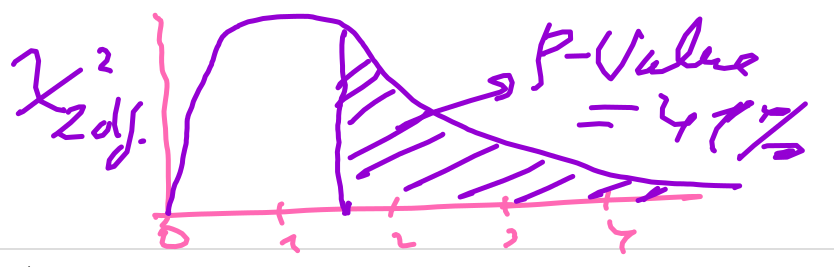
• valor-p = CDF.chisq( lower=1.76, upper=+infinito, df=2) =0.41

Conclusão: como o p-value é superior aos níveis usuais de significância então não se rejeita H0, isto é, o equilíbrio de Hardy-Weinberg é verificado para a situação no enunciado.

Para efetuar o teste com calculadora gráfica consulte teste de ajustamento de Pearson.