ex. 5.6
Foi recolhida aleatoriamente uma amostra de 12 folhas de um determinado tipo de árvore tendo-se registado o comprimento e a largura (em mm; dados no ficheiro folhas.csv.
Estudos anteriores validaram a normalidade do comprimento e da largura destas.
Largura |
Comprimento |
36 |
54 |
22 |
43 |
25 |
47 |
34 |
59 |
26 |
54 |
25 |
44 |
23 |
46 |
42 |
61 |
25 |
51 |
40 |
67 |
35 |
64 |
40 |
57 |
Responda às questões utilizando software ou calculadora gráfica.
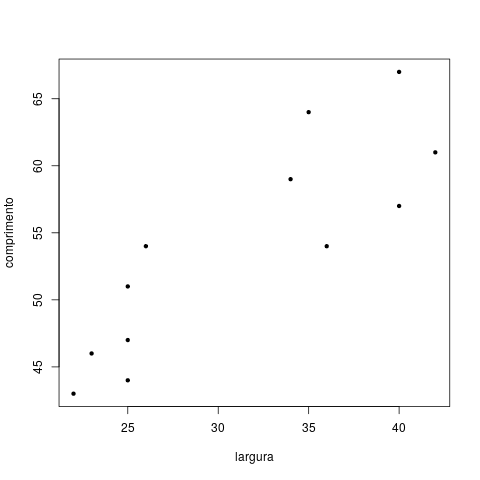
(a) Faça um gráfico de dispersão e explique a correlação positiva que nele se observa.
☞ sugestões
x = c(36, 22, 25, 34, 26, 25, 23, 42, 25, 40, 35, 40)
y = c(54, 43, 47, 59, 54, 44, 46, 61, 51, 67, 64, 57)
plot(x,y)
☞ solução
O gráfico de dispersão apresenta correlação positiva indicando que quanto maior o comprimento das folhas maior é a largura destas, em termos médios.
(b) Calcule o coeficiente de correlação de Pearson. Interprete o coeficiente no contexto do problema.
☞ sugestões
cor.test(x,y)
☞ solução
Obtemos \(r=0.858\) através dos resultados do sistema R:
Pearson's product-moment correlation
data: dados$comprimento and dados$largura
t = 5.2837, df = 10, p-value = 0.0001779
alternative hypothesis: true correlation is greater than 0
95 percent confidence interval:
0.6277347 1.0000000
sample estimates:
cor
0.858063
(c) Teste se o coeficiente de correlação é significativamente superior a zero, interpretando o resultado no contexto do problema.
☞ sugestões
A reflectir.
☞ solução
O coeficiente de correlação de Pearson é significativamente superior a zero (valor-p < 0.05):
e assim podemos assumir que as variáveis largura e comprimento da folha são significativamente correlacionadas de forma linear e crescente.