ex. 1.14

O ficheiro camaroes.csv contém uma amostra de valores correspondentes ao comprimento dos corpos de 60 camarões de aquacultura selecionados ao acaso.

(a) Classifique a variável em estudo.

☞ solução

Quantitativa contínua na escala de razões;

(b) A seguir apresentam-se uma análise exploratória dos dados, em R, com aquele ficheiro de dados:

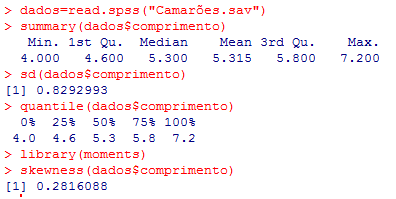
(b-i) Comente resumidamente a localização central (média e mediana), a dispersão (amplitude, desvio padrão e distância interquartil) e a simetria da distribuição (coeficiente de assimetria).

☞ solução

• Localização central: média $\bar x=5.315$ e mediana $m_e=5.3$.

• Dispersão: amplitude=7.2-4=3.2, desvio padrão corrigido $s_c=0.8292993$ e distância interquartil H=5.8-4.6=1.2.

• Simetria da distribuição: coeficiente de assimetria = 0.28, ie, ligeira assimetria positiva.

Verifica-se que $\bar x>m_e$ como é usual, mas nem sempre, nas distribuições com assimetria positiva: a média segue a tendência de valores mais elevados enquanto que a mediana tende a ser mais robusta a esses valores.

(b-ii) Indique o valor, à direita do qual, se encontram apenas 25% dos dados.

☞ solução

Trata-se do terceiro quartil, Q3=5.8.

☞ mostrar código R

dados <- read.csv("https://sweet.ua.pt/pedrocruz/dados/camaroes.csv",dec=",")
summary(dados$comprimento)
sd(dados$comprimento)
quantile(dados$comprimento)