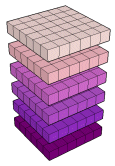
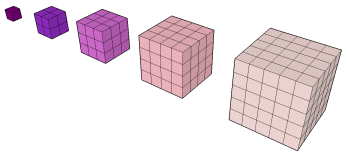Parte 7 : cubos
Números cúbicos(o primeiro e os outros)
Definição { cubo }:
A unidade é o primeiro cubo;
A soma de um cubo com o hexo de ordem seguinte é um cubo.
Notação { cubo de ordem n, n3 }:
13 := 1
(n+1)3 := n3 + hn+1
| |
43 = 33 + h4
|
|
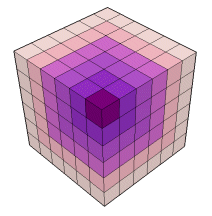
Propriedade:
O cubo de ordem n é a soma dos n primeiros hexos.
Notação:
n3 = h1 + h2 + h3 + ... + hn
Porque:
O primeiro cubo é o primeiro hexo;
O cubo de ordem n+1 é a soma dos n primeiros hexos,
somada com o hexo de ordem n+1.
| |
53 = h1 + h2 + h3 + h4 + h5
63 = h1 + h2 + h3 + h4 + h5 + h6
|
|
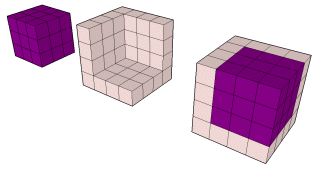
Portanto:
A diferença de dois cubos é uma soma de hexos consecutivos.
Notação:
m3 - n3 = hn+1 + hn+2 + ... + hm
| |
63 - 33 = h4 + h5 + h6
|

|
Propriedade:
O cubo de ordem n é n vezes o quadrado de ordem n.
Propriedade:
O cubo de ordem n é n vezes o prónico de ordem n-1 mais o quadrado de ordem n.
Notação:
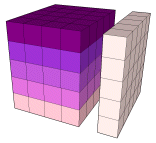
n3 = n x pn-1 + n2
| |
53 = 5 x p4 + 52
|
|
Porque:
pn-1 + n = n2
n x n2 = n3
Portanto:
O cubo de ordem n é uma soma de n ímpares consecutivos.
Porque:
pn-1 é um par,
n2 é uma soma de n ímpares consecutivos
e a soma de um par com um ímpar é um ímpar.
Propriedade:
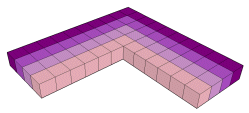
O cubo de ordem n é a soma dos n ímpares consecutivos,
que se seguem aos tn-1 primeiros ímpares.
Notação:
k = tn-1
n3 = ik+1 + ik+2 + ... + ik+n
| |
k = t3 = 6
43 = i7 + i8 + i9 + i10
|
|
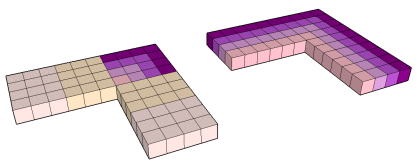
Porque:
n3 = n x pn-1 + n2 onde
pn-1 = 2 x tn-1 e
n2 = i1 + i2 + ... + in
n3 = (2 x tn-1 + i1) + (2 x tn-1 + i2) + ... + (2 x tn-1 + in)
| |
43 = 4 x 2 x t3 + i1 + i2 + i3 + i4
43 = i7 + i8 + i9 + i10
|
|
Portanto:
O primeiro ímpar é o cubo de 1
a soma dos 2 ímpares seguintes é o cubo de 2
a soma dos 3 ímpares seguintes é o cubo de 3
...
a soma dos n ímpares seguintes é o cubo de n
a soma dos n+1 ímpares seguintes é o cubo de n+1
...
| |
1 = 13 |
3+5 = 23 |
7+9+11 = 33 |
| |
13+15+17+19 = 43 |
21+23+25+27+29 = 53 |
31+33+35+37+39+41 = 63 |
| |
43+45+47+49+51+53+55 = 73 |
57+59+61+63+65+67+69+71 = 83 |
... |
| |
mas a soma dos primeiros n ímpares é o quadrado de n,
1+3+5+7+9+11+13+15+17+19+21+23+25+27+29 = 152 |

|
Propriedade:
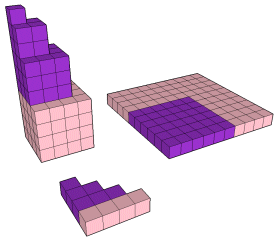
A soma dos n primeiros cubos é o quadrado do triângulo de ordem n.
Notação:
13 + 23 + 33 + ... + n3 =
tn2
Porque:
O primeiro ímpar é o primeiro cubo;
A soma dos n+1 ímpares consecutivos,
que se seguem aos tn primeiros ímpares é o cubo de ordem n+1.
| |
13 + 23 + 33 = t32
13 + 23 + 33 + 43 =
t42
|
|
Portanto:
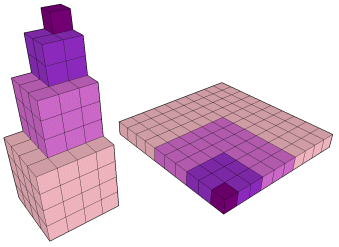
A soma dos n primeiros cubos é o quadrado da soma dos n primeiros números.
Notação:
13 + 23 + 33 + ... + n3 =
(1 + 2 + 3 + ... + n)2
| |
13 + 23 + 33 + 43 =
(1 + 2 + 3 + 4)2 |
|
Propriedade:
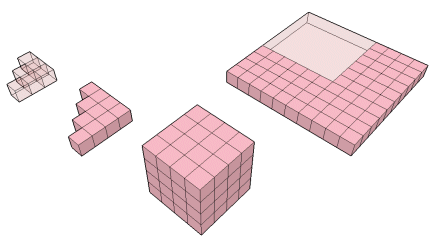
A diferença dos quadrados de dois triângulos consecutivos é um cubo.
Notação:
tn+12 - tn2 = (n+1)3
Porque:
tn+1 + tn = (n+1)2
tn+1 - tn = n+1
| |
t4 + t3 = 42
t4 - t3 = 4
t42 - t32 = 43
|
|
para outras partes:
(anterior)
1
2
3
4
5
6
7
(começar de novo)
{ Rosália Rodrigues, 2006 }